
心理学研究における欠測値処理を考える(長崎大学情報データ科学部准教授:高橋将宜) #心理統計を探検する
量的なデータを分析する際にまず問題となるのが,欠測値の処理です.しばしばとられる方法として,リストワイズ削除や平均値代入法などがあげられますが,こうした対応には実は問題があります。今回は高橋将宜先生に,こうした対処がもたらしうるバイアス,そして,代替となる欠損値処理の方法をご紹介いただきました.
南風原(2002, pp.6-7)は,心理学研究における統計分析について,反社会行動という変数を具体例として取り上げている.反社会行動は,社会秩序に反する多様な行動を表す抽象的な概念である.このように,心理学において研究対象となる変数は,直接的に測定することが困難なものが多いと考えられる.そこで,反社会行動のような興味の対象となる変数を抽象的に定義した上で,その定義に該当すると思われる複数の測定可能な項目を用意して,これらの測定可能な項目について被験者に質問をする.その後,これらの複数の項目の得点を合計して,もともとの興味の対象であった抽象的な変数を測定するといったことがよく行われる.ここで問題となり得ることは,測定可能な項目として用意した複数の質問のいくつかに対して,被験者が答えてくれない場合があることである.
このように欠測が問題となる場面において,鈴木(2018, p.139)は,心理学研究において欠測値の処理方法に言及をしていない論文が半数もあり,言及をしている場合でも,除去法や簡便な代入法を用いている場合が多いと報告している.そこで,本論考では,リストワイズ除去法や平均値代入法といった簡便な手法が解析結果にどのようなバイアス(偏り)をもたらすのか,また代替となる欠測値処理の方法を紹介する.
1. 完全データの統計解析
最初に,用語の整理をしておこう.完全データ(complete data)とは,調査計画どおりに得られたデータのことである.具体的には,表1.1のように,50人の被験者について,2つの変数($${y_1}$$と$${y_2}$$)があり,100個すべての値が適切に測定されて記録されているデータのことである.なお,表1.1におけるidは,個体を識別する番号であり,変数ではない.通常,大学初年級の入門的な統計学の授業で扱うデータは,$${\textsf{\textit{n}}}$$行×$${\textsf{\textit{p}}}$$列のすべての値が観測されている完全データであるから,読者にとって最もなじみ深いデータの形式であろう.
表1.1のデータは,いずれも平均50,標準偏差10,相関係数0.7の二変量正規分布に従う乱数として生成したものであるが,以下の議論を具体的に理解しやすくするために,具体的な意味づけをしておこう.$${y_1}$$は入学試験の英語の点数を偏差値にしたもの,$${y_2}$$は入学試験の国語の点数を偏差値にしたものとしておこう.
$$
表1.1:完全データ(\textrm{data01.csv}) \\[3pt]
\begin{array}{cccc|cccc} \hline
id & y_1 & y_2 & & & id & y_1 & y_2 \\ \hline
1 & 38.3 & 43.9 & & & 26 & 40.3 & 46.1 \\
2 & 50.4 & 44.2 & & & 27 & 56.0 & 65.4 \\
3 & 51.4 & 53.4 & & & 28 & 57.8 & 60.8 \\
4 & 46.1 & 32.6 & & & 29 & 53.2 & 45.5 \\
5 & 57.3 & 46.3 & & & 30 & 40.1 & 38.9 \\
6 & 52.0 & 48.5 & & & 31 & 51.6 & 65.0 \\
7 & 54.8 & 46.8 & & & 32 & 59.2 & 56.5 \\
8 & 55.0 & 65.6 & & & 33 & 54.0 & 59.4 \\
9 & 35.2 & 42.3 & & & 34 & 52.0 & 61.5 \\
10 & 64.7 & 58.6 & & & 35 & 43.7 & 49.8 \\
11 & 40.9 & 45.4 & & & 36 & 56.5 & 56.5 \\
12 & 36.0 & 43.1 & & & 37 & 61.1 & 62.8 \\
13 & 42.4 & 44.4 & & & 38 & 53.8 & 46.9 \\
14 & 51.0 & 53.7 & & & 39 & 39.3 & 42.7 \\
15 & 46.9 & 55.9 & & & 40 & 60.8 & 53.9 \\
16 & 49.0 & 45.3 & & & 41 & 60.6 & 53.9 \\
17 & 42.8 & 39.6 & & & 42 & 51.0 & 43.3 \\
18 & 40.3 & 47.7 & & & 43 & 68.2 & 63.1 \\
19 & 66.3 & 56.3 & & & 44 & 38.6 & 46.8 \\
20 & 51.1 & 52.6 & & & 45 & 54.7 & 51.7 \\
21 & 44.8 & 44.5 & & & 46 & 29.4 & 28.8 \\
22 & 39.5 & 43.1 & & & 47 & 50.3 & 46.7 \\
23 & 44.2 & 52.1 & & & 48 & 58.3 & 62.5 \\
24 & 33.6 & 35.7 & & & 49 & 42.2 & 49.4 \\
25 & 44.6 & 46.4 & & & 50 & 42.5 & 40.9 \\ \hline
\end{array}
$$
表1.1の完全データを集計してみよう.最も基本的な統計量である平均値(算術平均)を計算すると,以下のとおりである.完全データであれば,このような集計を行うことはたやすいものである.
$$
\\[1pt]
\bar y = \dfrac{1}{50}\sum\limits_{i=1}^{50} y_i
\\[1pt]
$$
$$
\\[1pt]
\bar y_1 = \dfrac{38.3+50.4+51.4+\dotsb+58.3+42.2+42.5}{50}\approx 49.1
\\[1pt]
$$
$$
\\[1pt]
\bar y_2 = \dfrac{43.9+44.2+53.4+\dotsb+62.5+49.4+40.9}{50}\approx 49.7
\\[1pt]
$$
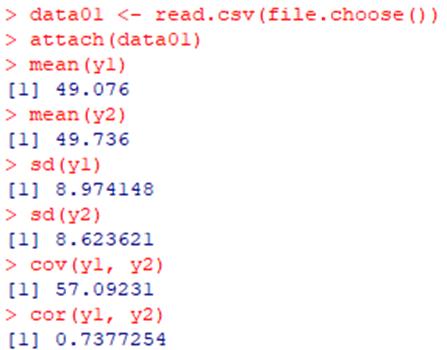
統計環境Rを用いると,以下のとおりに集計できる.標準偏差,共分散,相関係数といった他の統計量も一緒に出力してみよう.Rを用いた統計解析については,高橋・渡辺(2017,pp.1-9)などを参照されたい.なお,data01.csvは,表1.1の完全データであり,以下のURLから入手可能である.
https://www.kanekoshobo.co.jp/files/note/2023/sp_4/no_08/data01.csv
data01 <- read.csv(file.choose()) #data01.csvを読み込む
attach(data01) #data01を付置してアクティブにする
mean(y1) #y1の平均値
mean(y2) #y2の平均値
sd(y1) #y1の標準偏差
sd(y2) #y2の標準偏差
cov(y1, y2) #y1とy2の共分散
cor(y1, y2) #y1とy2の相関係数
2. 欠測データ解析の問題点
欠測(missing)とは,測定が欠けた状態のことであり,欠損や欠落ともいう.表2.1において,id番号1の変数$${y_2}$$の値は空欄となっている.このような値を欠測値といい,欠測の発生しているデータを欠測データという.表2.1では,変数$${y_2}$$の値が21個欠測している.
また,調査計画どおりに得られていないデータを不完全データ(incomplete data)といい,欠測データは不完全データの一種である.なお,不完全データは,欠測データ以外にも,一見するとすべての値が記録はされているものの,一部の値に誤りを含むデータのことも意味し得るが,本論考では欠測データと不完全データを同じ意味として扱うこととする.
$$
表2.1:欠測データ(\textrm{data02.csv}) \\[3pt]
\begin{array}{cccc|cccc} \hline
id & y_1 & y_2 & & & id & y_1 & y_2 \\ \hline
1 & 38.3 & & & & 26 & 40.3 & \\
2 & 50.4 & 44.2 & & & 27 & 56.0 & 65.4 \\
3 & 51.4 & 53.4 & & & 28 & 57.8 & 60.8 \\
4 & 46.1 & & & & 29 & 53.2 & 45.5 \\
5 & 57.3 & 46.3 & & & 30 & 40.1 & \\
6 & 52.0 & 48.5 & & & 31 & 51.6 & 65.0 \\
7 & 54.8 & 46.8 & & & 32 & 59.2 & 56.5 \\
8 & 55.0 & 65.6 & & & 33 & 54.0 & 59.4 \\
9 & 35.2 & 42.3 & & & 34 & 52.0 & 61.5 \\
10 & 64.7 & 58.6 & & & 35 & 43.7 & \\
11 & 40.9 & & & & 36 & 56.5 & 56.5 \\
12 & 36.0 & & & & 37 & 61.1 & 62.8 \\
13 & 42.4 & & & & 38 & 53.8 & 46.9 \\
14 & 51.0 & 53.7 & & & 39 & 39.3 & \\
15 & 46.9 & & & & 40 & 60.8 & 53.9 \\
16 & 49.0 & 45.3 & & & 41 & 60.6 & 53.9 \\
17 & 42.8 & & & & 42 & 51.0 & 43.3 \\
18 & 40.3 & & & & 43 & 68.2 & 63.1 \\
19 & 66.3 & 56.3 & & & 44 & 38.6 & \\
20 & 51.1 & 52.6 & & & 45 & 54.7 & 51.7 \\
21 & 44.8 & & & & 46 & 29.4 & \\
22 & 39.5 & 43.1 & & & 47 & 50.3 & \\
23 & 44.2 & & & & 48 & 58.3 & 62.5 \\
24 & 33.6 & & & & 49 & 42.2 & \\
25 & 44.6 & & & & 50 & 42.5 & \\ \hline
\end{array}
$$
表2.1の欠測データの集計をしてみよう.平均値を計算すると,以下のとおりである.
$$
\\[1pt]
\bar y_1 = \dfrac{38.3+50.4+51.4+\dotsb+58.3+42.2+42.5}{50}\approx 49.1
\\[1pt]
$$
$$
\\[1pt]
\bar y_2 = \dfrac{y_{2,1}+44.2+53.4+\dotsb+62.5+y_{2,49}+y_{2,50}}{50}=\dfrac{1565.4+y_{2,miss}}{50}=\space ?
\\[1pt]
$$
$${\bar{y}_1}$$は完全データの場合と同じ値として計算できているが,$${\bar y_2}$$は未知数$${y_{2,miss}}$$を含んでおり,計算することができない.ここで,$${y_{2,miss}}$$は,$${y_2}$$の欠測値の部分を表すこととする.つまり,$${y_{2,miss}}$$とは,以下のとおり,21個の未知数である.
$$
y_{2,miss}=
\begin{Bmatrix}
y_{2,1},y_{2,4},y_{2,11},y_{2,12},y_{2,13},y_{2,15},y_{2,17},y_{2,18},y_{2,21},y_{2,23},y_{2,24}, \\ y_{2,25},y_{2,26},y_{2,30},y_{2,35},y_{2,39},y_{2,44},y_{2,46},y_{2,47},y_{2,49},y_{2,50}
\end{Bmatrix}
$$
さらに,$${y_2}$$の標準偏差$${\textrm{sd}(y_2)}$$を計算しようとすると,上記で$${\bar{y_2}}$$が計算できていないことから,$${\textrm{sd}(y_2)}$$も計算できないことがわかる.
$$
\textrm{sd}(y_2)=\sqrt{\dfrac{1}{50-1}\sum\limits_{i=1}^{50}(y_{2i}-\bar{y_2})^2}=\space?
$$
二変量の解析をしたいとする.$${y_1}$$と$${y_2}$$の共分散の式にも$${\bar{y_2}}$$が登場するので,やはり共分散$${\textrm{cov}(y_1,y_2)}$$も計算できない.共分散$${\textrm{cov}(y_1,y_2)}$$と標準偏差$${\textrm{sd}(y_2)}$$が計算できないことから,相関係数$${\textrm{cor}(y_1,y_2)}$$も計算できないことがわかる.
$$
\textrm{cov}(y_1,y_2)=\dfrac{1}{50}\sum\limits_{i=1}^{50}(y_{1i}-\bar{y_1})(y_{2i}-\bar{y_2})=\space ?
$$
$$
\textrm{cor}(y_1,y_2)=\dfrac{\textrm{cov}(y_1,y_2)}{\textrm{sd}(y_1)\textrm{sd}(y_2)}=\space ?
$$
すなわち,データに欠測が発生している場合,ありとあらゆる統計解析が不可能になるのである.
統計環境Rを用いて集計する方法は以下のとおりであるが,やはり$${y_2}$$の平均値と標準偏差,共分散,相関係数はNA(Not Available)となっており,計算できていないことが示されている.なお,data02.csvは,表2.1の欠測データであり,以下のURLから入手可能である.第1節で使用したRのセッションは閉じて,新たにRを起ち上げ直して実行しよう.
https://www.kanekoshobo.co.jp/files/note/2023/sp_4/no_08/data02.csv
data02 <- read.csv(file.choose()) #data02.csvを読み込む
attach(data02) #以下のコードの意味は上記と同様
mean(y1)
mean(y2)
sd(y1)
sd(y2)
cov(y1, y2)
cor(y1, y2) 
本論考では,欠測メカニズムについての解説をするだけの紙面の余裕がないが,MCAR(Missing Completely At Random),MAR(Missing At Random),NMAR(Not Missing At Random)といった欠測メカニズムについては,高橋・渡辺(2017,pp.15-21)を参照されたい.
なお,表2.1のデータは,MARのメカニズムに基づく欠測データである.第1節で具体的な状況設定をしたとおり,$${y_1}$$は入学試験の英語の点数を偏差値にしたもの,$${y_2}$$は入学試験の国語の点数を偏差値にしたものとする.午前中の英語の試験を受けた後で,試験の出来が悪かった下位半分の受験者のうち80%が,合格を諦めて,午後の国語の試験を受けずに帰ってしまった状況として設定したものである.
3. 除去法の問題点
前節の結論では,データに欠測が発生している場合,ありとあらゆる統計解析が不可能になると述べた.
ところが,読者の中には,「欠測の発生しているデータを統計ソフトウェアに読み込んでも,統計量の計算ができなかったことはない」と思う人がいるだろう.しかし,それは,多くの統計ソフトウェアが除去法(削除法)という方法論を暗黙のうちに背後で使用しているからである.表2.1のように欠測が発生している場合に,欠測の発生している行を削除する方法をリストワイズ除去法(listwise deletion)という.リストワイズ除去法を実行したあとのデータは,一見すると「完全データ」のように見えることから,完全ケース分析(complete-case analysis)ともいう.
表3.1は,表2.1の欠測データに対してリストワイズ除去法を施したものである.被験者id 1,4,11,12,13,15,17,18,21,23,24,25,26,30,35,39,44,46,47,49,50の21人は削除されていて,掲載されていないことがわかるだろう.
$$
表3.1:リストワイズ除去(完全ケース分析) \\[3pt]
\begin{array}{cccc|cccc} \hline
id & y_1 & y_2 & & & id & y_1 & y_2 \\ \hline
2 & 50.4 & 44.2 & & & 29 & 53.2 & 45.5 \\
3 & 51.4 & 53.4 & & & 31 & 51.6 & 65.0 \\
5 & 57.3 & 46.3 & & & 32 & 59.2 & 56.5 \\
6 & 52.0 & 48.5 & & & 33 & 54.0 & 59.4 \\
7 & 54.8 & 46.8 & & & 34 & 52.0 & 61.5 \\
8 & 55.0 & 65.6 & & & 36 & 56.5 & 56.5 \\
9 & 35.2 & 42.3 & & & 37 & 61.1 & 62.8 \\
10 & 64.7 & 58.6 & & & 38 & 53.8 & 46.9 \\
14 & 51.0 & 53.7 & & & 40 & 60.8 & 53.9 \\
16 & 49.0 & 45.3 & & & 41 & 60.6 & 53.9 \\
19 & 66.3 & 56.3 & & & 42 & 51.0 & 43.3 \\
20 & 51.1 & 52.6 & & & 43 & 68.2 & 63.1 \\
22 & 39.5 & 43.1 & & & 45 & 54.7 & 51.7 \\
27 & 56.0 & 65.4 & & & 48 & 58.3 & 62.5 \\
28 & 57.8 & 60.8 & & & & & \\ \hline
\end{array}
$$
表3.1のリストワイズ除去したデータを集計してみよう.平均値を計算するが,今回は標本サイズが50ではなく,21人を削除したので残りは29であることに注意をしよう.計算結果は以下のとおりである.
$$
\\[1pt]
\bar y = \dfrac{1}{29}\sum\limits_{i=1}^{29} y_i
\\[1pt]
$$
$$
\\[1pt]
\bar y_1 = \dfrac{50.4+51.4+57.3+\dotsb+68.2+54.7+58.3}{29}\approx 54.7
\\[1pt]
$$
$$
\\[1pt]
\bar y_2 = \dfrac{44.2+53.4+46.3+\dotsb+63.1+51.7+62.5}{29}\approx 54.0
\\[1pt]
$$
表3.1は,一見すると「完全データ」と同じデータ形式であることから,$${\bar{y_1}}$$と$${\bar{y_2}}$$の両方とも数値として計算することができている.しかしながら,第1節の集計結果より,完全データの場合の$${\bar{y_1}}$$の値は49.1であり,$${\bar{y_2}}$$の値は49.7であった.リストワイズ除去をした後の$${\bar{y_1}}$$と$${\bar{y_2}}$$は,いずれも,完全データの場合の値とは異なり,過大な値となっている.この2つの値が間違った値であるということは,第2節で見たとおり,標準偏差,共分散,相関係数もすべて間違った値になることを含意している.
統計環境Rを用いると,以下のとおりに集計できるが,完全データの場合と比べて,確かにすべての統計量は間違った値になっていることがわかる.なお,data02.csvは,表2.1の欠測データである.第2節で使用したRのセッションは閉じて,新たにRを起ち上げ直して実行しよう.
data02 <- read.csv(file.choose()) #data02.csvを読み込む
data02b <- na.omit(data02) #欠測値(NA)を省略(omit)する
attach(data02b) #以下のコードの意味は上記と同様
mean(y1)
mean(y2)
sd(y1)
sd(y2)
cov(y1, y2)
cor(y1, y2)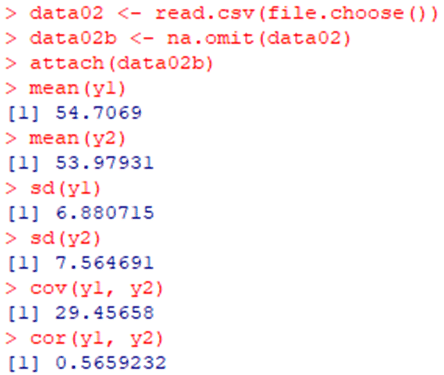
4. 平均値代入法の問題点
ここまでの議論から,欠測データはそのままでは解析が不可能であり,欠測している行を削除した解析は誤った解析結果になることがわかった.未知数である欠測値を,適当な値に置き換える方法を代入法(imputation)という.補完法や補定法ともいう.
たとえば,日本人の成人男性の平均身長は約170 cmである.日本人の成人男性から無作為にAさんを抽出したとしよう.このとき,Aさんの身長は何センチであろうか? 利用できる情報がここに示されているものだけならば,Aさんの身長を予測する最良の値は平均値170 cmである.
被験者id 1の変数$${y_2}$$の値は,上記のAさんの身長と同様に未知数である.つまり,変数$${y_2}$$の残り29人分のデータから平均値を計算した値が最良の予測値と考えることは,ごく自然な発想のように思われるだろう.前節で計算したとおり,その値は54.0であった.このように,欠測値を残りのデータの平均値に置き換える方法を平均値代入法(mean imputation)という.表4.1は,表2.1の欠測データに対して平均値代入法を施したものである.
$$
表4.1:平均値代入法(\textrm{data03.csv})\\ \\[3pt]
\begin{array}{cccc|cccc} \hline
id & y_1 & y_2 & & & id & y_1 & y_2 \\ \hline
1 & 38.3 & \fcolorbox{black}{black}{54.0} & & & 26 & 40.3 & \fcolorbox{black}{black}{54.0} \\
2 & 50.4 & 44.2 & & & 27 & 56.0 & 65.4 \\
3 & 51.4 & 53.4 & & & 28 & 57.8 & 60.8 \\
4 & 46.1 & \fcolorbox{black}{black}{54.0} & & & 29 & 53.2 & 45.5 \\
5 & 57.3 & 46.3 & & & 30 & 40.1 & \fcolorbox{black}{black}{54.0} \\
6 & 52.0 & 48.5 & & & 31 & 51.6 & 65.0 \\
7 & 54.8 & 46.8 & & & 32 & 59.2 & 56.5 \\
8 & 55.0 & 65.6 & & & 33 & 54.0 & 59.4 \\
9 & 35.2 & 42.3 & & & 34 & 52.0 & 61.5 \\
10 & 64.7 & 58.6 & & & 35 & 43.7 & \fcolorbox{black}{black}{54.0} \\
11 & 40.9 & \fcolorbox{black}{black}{54.0} & & & 36 & 56.5 & 56.5 \\
12 & 36.0 & \fcolorbox{black}{black}{54.0} & & & 37 & 61.1 & 62.8 \\
13 & 42.4 & \fcolorbox{black}{black}{54.0} & & & 38 & 53.8 & 46.9 \\
14 & 51.0 & 53.7 & & & 39 & 39.3 & \fcolorbox{black}{black}{54.0} \\
15 & 46.9 & \fcolorbox{black}{black}{54.0} & & & 40 & 60.8 & 53.9 \\
16 & 49.0 & 45.3 & & & 41 & 60.6 & 53.9 \\
17 & 42.8 & \fcolorbox{black}{black}{54.0} & & & 42 & 51.0 & 43.3 \\
18 & 40.3 & \fcolorbox{black}{black}{54.0} & & & 43 & 68.2 & 63.1 \\
19 & 66.3 & 56.3 & & & 44 & 38.6 & \fcolorbox{black}{black}{54.0} \\
20 & 51.1 & 52.6 & & & 45 & 54.7 & 51.7 \\
21 & 44.8 & \fcolorbox{black}{black}{54.0} & & & 46 & 29.4 & \fcolorbox{black}{black}{54.0} \\
22 & 39.5 & 43.1 & & & 47 & 50.3 & \fcolorbox{black}{black}{54.0} \\
23 & 44.2 & \fcolorbox{black}{black}{54.0} & & & 48 & 58.3 & 62.5 \\
24 & 33.6 & \fcolorbox{black}{black}{54.0} & & & 49 & 42.2 & \fcolorbox{black}{black}{54.0} \\
25 & 44.6 & \fcolorbox{black}{black}{54.0} & & & 50 & 42.5 & \fcolorbox{black}{black}{54.0} \\ \hline
\end{array} \\ \\[3pt]
注:枠で囲われた数字は,欠測値を平均値代入法で処理した値である.
$$
表4.1の平均値代入法を適用したデータを集計してみよう.これまでと同じように,平均値を計算する.今回は50行×2列のすべてのセルに値が埋まっている状態なので,標本サイズは50である.計算結果は以下のとおりである.
$$
\\[1pt]
\bar{y}=\dfrac{1}{50}\sum\limits_{i=1}^{50}y_i
\\[1pt]
$$
$$
\\[1pt]
\bar{y_2}=\dfrac{1565.4+21\times 54.0}{50}\approx 54.0
\\[1pt]
$$
統計環境Rを用いると,以下のとおりに集計できる.なお,data03.csvは,表4.1の平均値代入法を適用したデータであり,以下のURLから入手可能である.第3節で使用したRのセッションは閉じて,新たにRを起ち上げ直して実行しよう.
https://www.kanekoshobo.co.jp/files/note/2023/sp_4/no_08/data03.csv
data03 <- read.csv(file.choose()) #data03.csvを読み込む
attach(data03) #以下のコードの意味は上記と同様
mean(y2)
sd(y2)
cor(y1, y2)
この結果から,平均値代入法を適用しても,リストワイズ除去法による平均値と比較して,集計結果は改善していないことがわかる.実は,集計結果が改善しないどころか,表4.2のとおり,標準偏差や相関係数といった他の統計量については,結果をさらに悪くしてしまうのである.なお,完全データの標準偏差が8.60となっているのは,1回限りの標本抽出による誤差である(表5.2を参照).
$$
表4.2:集計結果 \\ \\[3pt]
\begin{array}{l|rrrr} \hline
& 真値 & 完全データ & リストワイズ & 平均値代入法 \\ \hline
平均値 & 50.00 & 49.70 & 54.00 & 54.00 \\
標準偏差 & 10.00 & 8.60 & 7.60 & 5.72 \\
相関係数 & 0.70 & 0.74 & 0.57 & 0.33 \\ \hline
\end{array}
$$
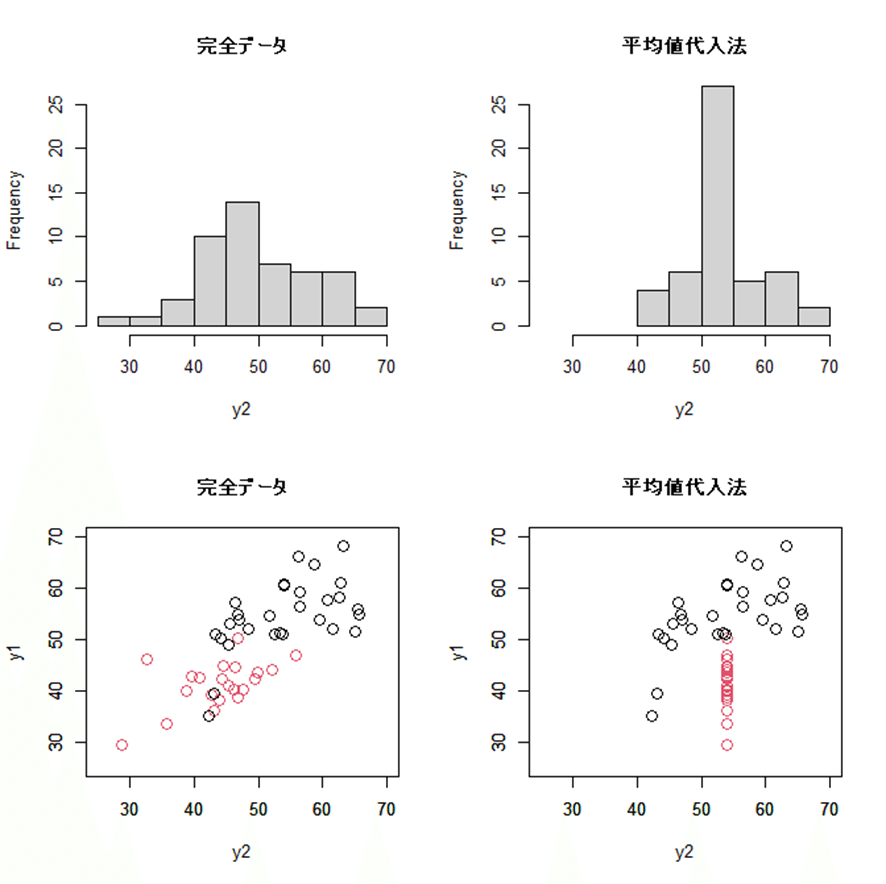
なぜ,標準偏差や相関係数に対して,このような悪影響が出るのか,理由を考えてみよう.図4.1には,左側に完全データの場合のヒストグラムと散布図が図示されており,右側に平均値代入法の場合のヒストグラムと散布図が図示されている.今回の欠測データでは,50個の観測値のうち21個が欠測していた.平均値代入法では,これら21個すべてに対して54.0という同じ値を代入しているため,ヒストグラムでは54.0のところのバーがとても高くなっていることがわかる.また,もともとの完全データでは,25付近から70付近までデータがあったのに対して,平均値代入法では,40付近から70付近までしかデータがない.したがって,平均値代入法では,ばらつきの大きさに悪影響が出ているのである.また,散布図では,欠測値を赤丸で表示しており,完全データの散布図と比較して,平均値代入法の散布図では赤丸が縦軸に対して平行に一直線で並んでいる.つまり,これら21個の値は,横軸の$${y_2}$$のばらつきがゼロであるから,$${y_1}$$との相関がないことになってしまっているのである.したがって,$${y_1}$$と$${y_2}$$の相関係数が過小に推定されている.
以上のとおり,平均値代入法には,百害あって一利もないのである(高井・星野・野間,2016,p.6;高橋・渡辺,2017,p.32).
5. 多重代入法による解決
このような欠測データの問題を解決するための一般的な方法論として,多重代入法(multiple imputation)が知られている.上記の解析結果は,多重代入法を用いることによって表5.1のとおりに改善され得る.
$$
表5.1:集計結果(多重代入法) \\ \\[3pt]
\begin{array}{l|rrrrr}\hline
& 真値 & 完全データ & リストワイズ & 平均値代入法 & 多重代入法 \\ \hline
平均値 & 50.00 & 49.70 & 54.00 & 54.00 & 50.56 \\
標準偏差 & 10.00 & 8.60 & 7.60 & 5.72 & 8.36 \\
相関係数 & 0.70 & 0.74 & 0.57 & 0.33 & 0.66 \\ \hline
\end{array}
$$
多重代入法の詳しい解説は専門書(高橋・渡辺,2017;高井・星野・野間,2016,pp.102-140;阿部,2016,pp.93-124)に譲るが,統計環境Rを用いて集計する方法は以下のとおりである.なお,相関係数の集計には,Schafer(1997)より,フィッシャーのz変換を用いるべきであるが,以下では簡便に基本統計量で表示している.なお,data02.csvは,表2.1の欠測データである.第4節で使用したRのセッションは閉じて,新たにRを起ち上げ直して実行しよう.
install.packages("Amelia") #RパッケージAmeliaのインストール
#この作業は一度だけ実行すればよい
data02 <- read.csv(file.choose()) #data02.csvを読み込む
attach(data02)
library(Amelia) #RパッケージAmeliaの読み込み
#この作業は毎回実行する
set.seed(1) #乱数のシード値の設定
a.out <- amelia(data02, m=100, p2s=0) #多重代入法の実行
#m = 100で100回の多重代入
#p2s = 0で代入プロセスを非表示
mean3 <- NULL #ループ内の結果を格納する空の変数
sd3 <- NULL #ループ内の結果を格納する空の変数
cor3 <- NULL #ループ内の結果を格納する空の変数
for(i in 1:100){ #iを1から100まで繰り返すループ
y3b <- a.out$imputations[[i]]$y2 #i番目の代入済みデータのy2
mean3[i] <- mean(y3b) #平均値
sd3[i] <- sd(y3b) #標準偏差
cor3[i] <- cor(y1, y3b) #相関係数 } #ループの終わり
mean(mean3) #100個の平均値の統合
summary(sd3) #100個の標準偏差の基本統計量
summary(cor3) #100個の相関係数の基本統計量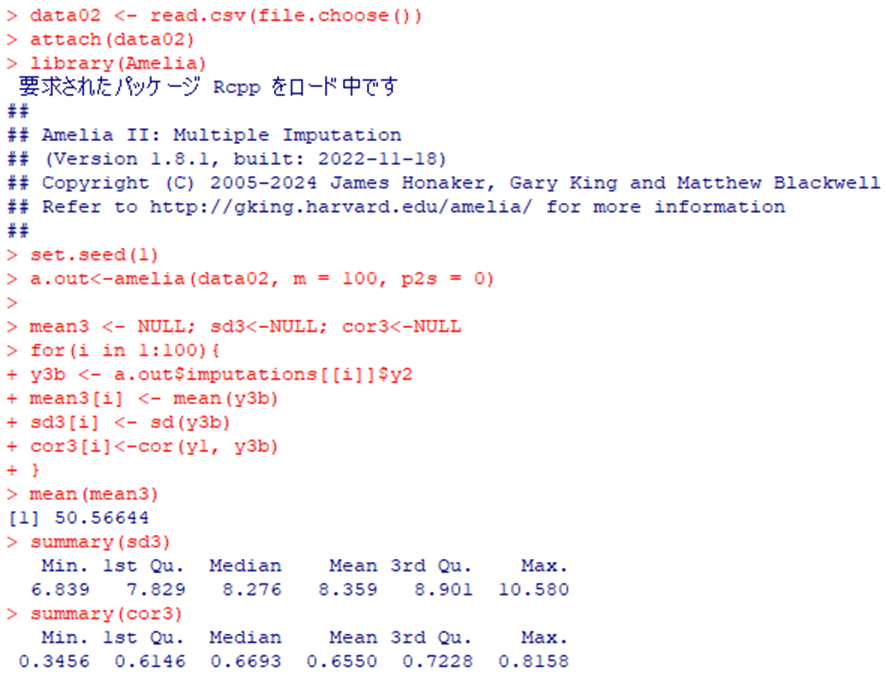
本論考で設定した乱数と同様の演算を1000回繰り返したモンテカルロ・シミュレーションの結果を表5.2に示す.この結果からわかるとおり,完全データおよび多重代入法による結果は,真値を適切に推定すること可能である.一方,リストワイズ除去法および平均値代入法にはバイアス(偏り)があることがわかる.
$$
表5.2:モンテカルロ・シミュレーション(1000回)の結果 \\ \\[3pt]
\begin{array}{l|rrrrrrr}\hline
& 真値 & 完全データ & リストワイズ & 平均値代入法 & 多重代入法 \\ \hline
平均値 & 50.00 & 49.98 & 53.66 & 53.66 & 49.97 \\
標準偏差 & 10.00 & 9.95 & 9.18 & 7.09 & 9.91 \\
相関係数 & 0.70 & 0.70 & 0.66 & 0.41 & 0.69 \\ \hline
\end{array}
$$
多重代入法のメカニズムやアルゴリズムを説明することは,本論考の範疇を超えるため,詳しくは高橋・渡辺(2017,pp.38-71)を参照されたい.また,欠測データを用いた平均値の$${\textsf{\textit{t}}}$$検定,重回帰分析,共分散分析,ロジスティック回帰分析,時系列分析,パネルデータの分析については,高橋・渡辺(2017,pp.82-154)を参照されたい.さらに,交互作用項のあるモデル,傾向スコアマッチング,操作変数法,回帰不連続デザインにおける欠測データへの対処法については,高橋(2022,pp.263-293)を参照されたい.
謝辞
本論考執筆に関する情報収集などには,JSPS科研費・基盤研究(C)No.23K11010の援助を受けた.また,宮本江里菜氏(長崎大学大学院)には,本論考の草稿を閲読していただき,有益なコメントをいただいたことに感謝したい.
参考文献
阿部貴行(2016)『欠測データの統計解析』,朝倉書店.
Schafer, J. L.(1997)Analysis of Incomplete Multivariate Data, Chapman & Hall/CRC.
鈴木雅之(2018)「測定・評価・研究法に関する研究動向と展望:統計的分析手法の利用状況と評価リテラシーの育成に向けて」,『教育心理学年報』vol.57, pp.136-154.
高井啓二・星野崇宏・野間久史(2016)『欠測データの統計科学』,岩波書店.
高橋将宜・渡辺美智子(2017)『欠測データ処理:Rによる単一代入法と多重代入法』,共立出版.
高橋将宜(2022)『統計的因果推論の理論と実装:潜在的結果変数と欠測データ』,共立出版.
南風原朝和(2002)『心理統計学の基礎:統合的理解のために』,有斐閣アルマ.
執筆者プロフィール
高橋将宜(たかはし・まさよし)
長崎大学 情報データ科学部 准教授.
2017年9月に成蹊大学大学院にて博士(理工学)を取得.2017年12月には『欠測データ処理:Rによる単一代入法と多重代入法』を共立出版から出版し,2019年度経済統計学会賞を受賞した.2022年2月には『統計的因果推論の理論と実装:潜在的結果変数と欠測データ』を共立出版から出版した.
独立行政法人統計センター上級研究員,鹿児島国際大学経済学部准教授などを経て,2020年4月より現職.
専門は,統計科学・計量政治学で,主に統計的因果推論と欠測データ解析に関する方法論的研究を行っている.

