重回帰分析の数理モデル

　先に記したように，重回帰分析は（同時に分析に組み入れる）説明変数の数が２以上である場合の回帰分析であり，説明変数の数が２である場合，一般に，次式のような説明変数の１次式によって基準変数の値を予測ないし説明しようとします（本稿では，以下，もっとも基本的なケースである説明変数の数が２である場合で説明を行ないます）。

$$
\hat{y}=a+b_1x_1+b_2x_2
$$

　上記の式における各説明変数の重み係数とも言える１次の係数$${b_1}$$，$${b_2}$$ が本稿の主たる説明対象である偏回帰係数ですが，それについての説明は後にして，ここではまず，「上記のような１次式によって予測ないし説明を行なうということは，重回帰分析では，各説明変数（$${x_1}$$，$${x_2}$$）と基準変数（$${y}$$）の間にどのような関係があることを（誤差のない，理想的な状態として）想定していることになるのか」，言い換えれば，「重回帰分析では，データがどのようになっているときに，全ての対象においてまったく誤差がなく，完全な予測ないし説明ができることになるのか」ということについて説明します。

　たとえば，上記の式において$${a=-2}$$，$${b_1=2}$$，$${b_2=3}$$であるとします。そうすると，$${x_2}$$の値の変化に対応して，$${x_1}$$と$${y}$$の関係式は次のようになります（ここでは，予測の誤差がない場合の「各説明変数と基準変数の間の関係についての想定」に関して説明しているため，基準変数を，予測値である$${\hat{y}}$$ではなく，観測値である$${y}$$として記述します）。[1]

$$
\begin{array}{cc}
x_2=1\spaceのとき & y=1+2x_1 \\
x_2=2\spaceのとき & y=4+2x_1 \\
x_2=3\spaceのとき & y=7+2x_1 \\
\vdots & \vdots
\end{array}
$$

　以上の例が示しているように，重回帰分析では，$${\textbf{\textit{x}}_\textbf{2}}$$の値が一定であれば（言い換えれば，$${\textbf{\textit{x}}_\textbf{2}}$$が各々の値である場合においては）$${\textbf{\textit{x}}_\textbf{1}}$$と$${\textbf{\textit{y}}}$$の間に直線的関係が存在している（一般的に言えば，他の説明変数の値が一定に統制されていれば各説明変数と基準変数の間には直線的関係が存在する）ことが想定されていることになります。また，$${x_1}$$の変化に伴う$${y}$$の変化の様相を示すものである$${\textbf{\textit{x}}_\textbf{1}}$$の１次の係数の値は，$${\textbf{\textit{x}}_\textbf{2}}$$（すなわち，他の説明変数）の値がいくらであっても変わらない（上記の場合は，常に$${b_1}$$の値である２である）ことも想定されていることになります。[2] さらに，切片の値は$${\textbf{\textit{x}}_\textbf{2}}$$の値の変化に伴って１次関数的に変化する（言い換えれば，各$${\textbf{\textit{x}}_\textbf{2}}$$の値における$${\textbf{\textit{x}}_\textbf{1}}$$から$${\textbf{\textit{y}}}$$を予測する際の回帰直線の切片の値と当該の$${\textbf{\textit{x}}_\textbf{2}}$$の値の間には直線的関係が存在している）ことも想定されていることになります（上記の例では，$${x_2}$$の値が１大きくなると，切片の値が$${b_2}$$の値である３ずつ大きくなります）。ただし，以下でも留意するよう記しますが，$${b_1}$$の値は，「$${x_1}$$$${\underline{\textrm{の変化に伴う}}}$$$${y}$$の$${\underline{\textrm{変化}}}$$の様相を示すものである」というよりも，「$${x_1}$$における１の$${\underline{\textrm{差異が}}}$$$${y}$$におけるいくらの$${\underline{\textrm{差異に対応しているか}}}$$を表わしている」と表現した方が適切（ないし，無難）であるものです。[3]

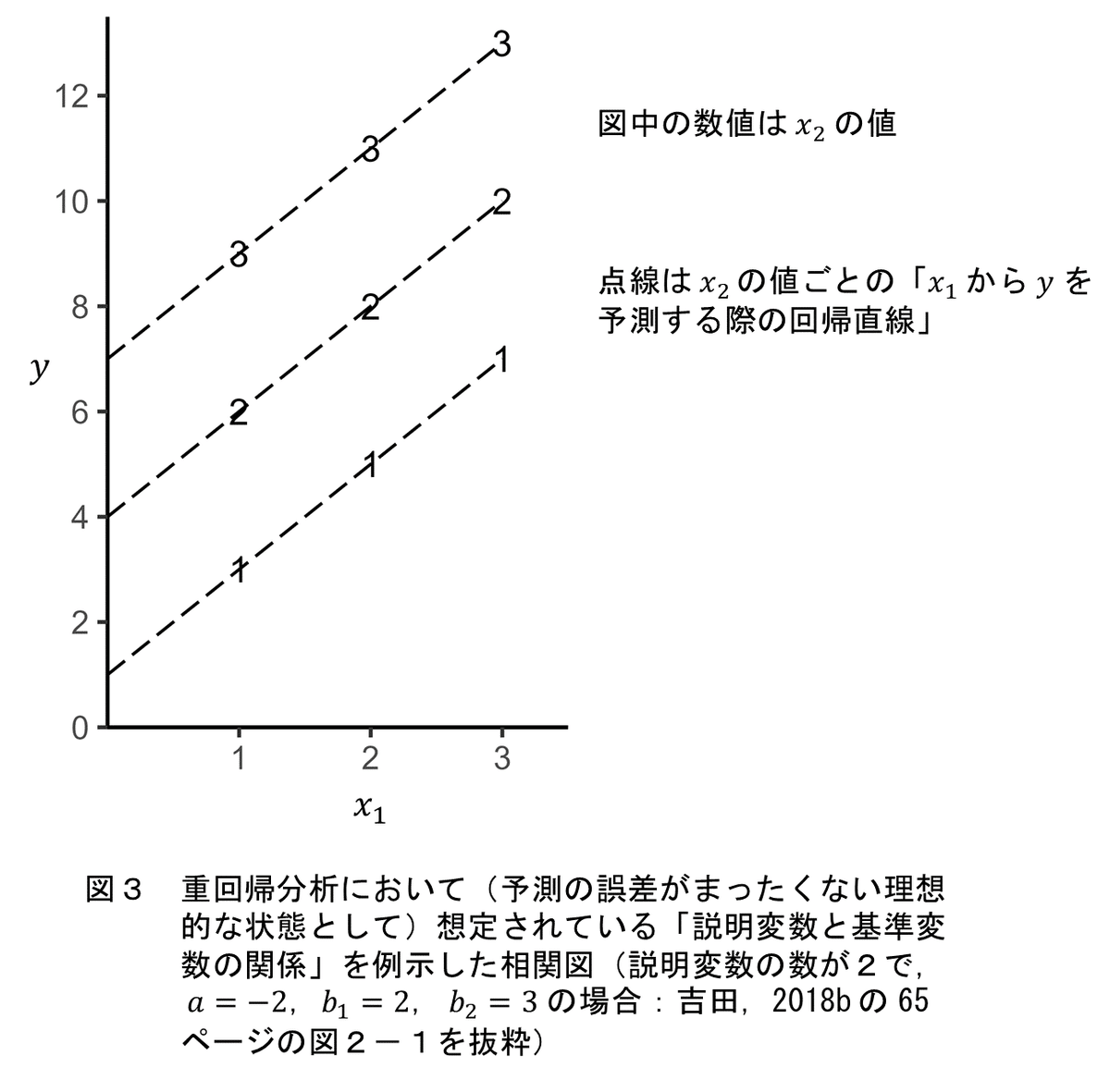
　以上のことから，重回帰分析では，図３の相関図に示したような状態になることを想定していることになり，このような状態を数式化した上記の式による$${y}$$の予測値である$${\hat{y}}$$と実際に得られた値である$${y}$$が全ての対象において完全に一致しているときに，予測の誤差がまったくない理想的な状態であることになります。[4]

偏回帰係数という値の意味

　「$${x_1}$$の偏回帰係数である$${b_1}$$が，$${x_2}$$の値が一定であるときの$${x_1}$$と$${y}$$の関係を表わすものである」ということを示唆する前項での説明から，先に意味を説明した「予測の誤差というもの」が「偏回帰係数というもの」に強く関わっていることが推察されると思います。ここでは，このこと（すなわち，予測の誤差と偏回帰係数の関わり）について詳しく説明します。[5]

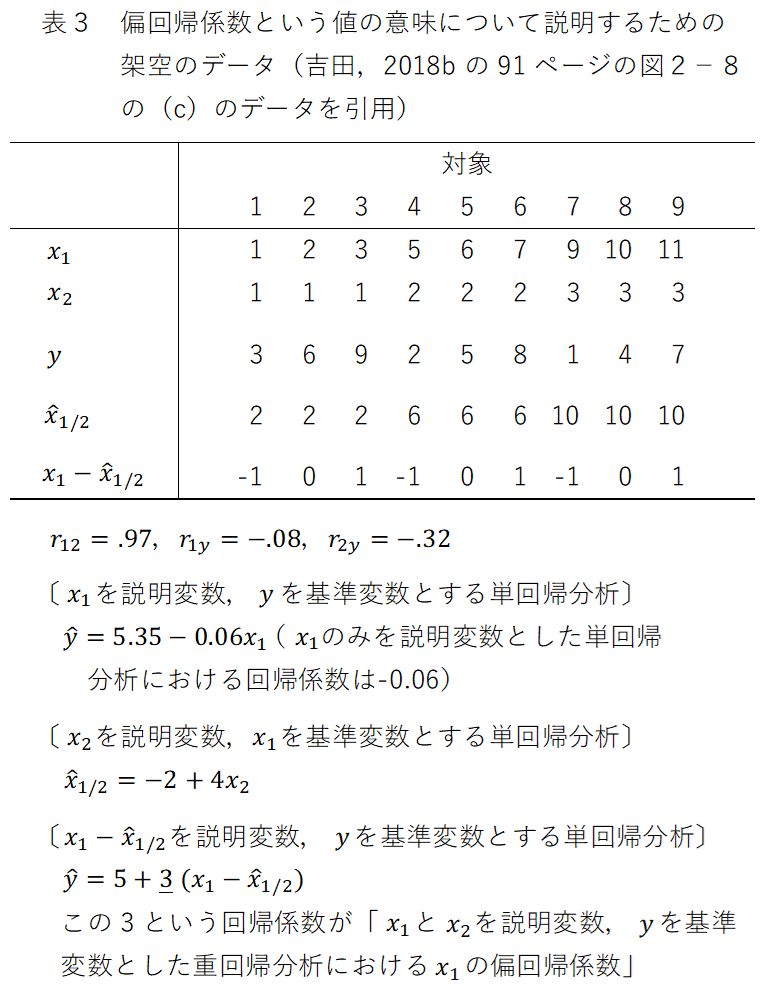
　まず，表３のデータ，および，それの相関図である図４を見てください。各対象の$${x_2}$$の値を考慮せずに，全データにおける$${x_1}$$と$${y}$$の関係について分析すると，図４から視認されるように，$${x_1}$$と$${y}$$の相関係数および$${x_1}$$から$${y}$$を予測する単回帰分析における回帰係数は負の値になります（具体的には，$${r=-.08}$$，$${b=-0.06}$$になります）。[6] したがって，このデータでは，（$${x_1}$$から見て他の説明変数である）$${x_2}$$の値を考慮しない場合，$${x_1}$$と$${y}$$の間には，（「関係が認められない」とする方が適切であろうところをあえて記しますが）「（非常に弱いながらも）$${x_1}$$の値が大きいほど$${y}$$の値が小さい」という関係があることになります。これに対して，$${x_2}$$を一定にすると（言い換えれば，$${x_2}$$の値が１，２，３の各々である場合ごとに検討すると），$${x_1}$$から$${y}$$を予測する単回帰分析における（切片の値が$${x_2}$$の値の変化に伴って１次関数的に変化しているとともに）回帰直線の傾きがいずれも３になっている（すなわち，$${x_1}$$における１の差異が$${y}$$における３の差異と対応している）ので，$${x_1}$$の偏回帰係数である$${b_1}$$は３（という正の値）になります。

　以上のことが例示しているように，「１つの変数のみを説明変数とした単回帰分析における回帰係数」と「その変数に加えて他の変数も組み入れた重回帰分析における（最初の説明変数の）偏回帰係数」は，通常，同じ値にはなりません。そして，場合によっては，上記の例のように，符号が逆になることもあります。したがって，重回帰分析における偏回帰係数は，各々の説明変数と基準変数の単純な関係を表わしているものではないことになります。では，偏回帰係数は，どのように算出され，どのような意味を持つものなのでしょうか。以下では，このような「偏回帰係数の意味（正体？）」ということについて詳しく説明します。

　さて，重回帰分析においてある説明変数の偏回帰係数の値を求める際には，まず，説明変数同士の中で回帰分析（説明変数の数が２である場合は単回帰分析，３以上の場合は重回帰分析）を行ないます。具体的には，偏回帰係数を求める対象となる説明変数を基準変数，それ以外の説明変数を説明変数とする回帰分析であり，説明変数が$${x_1}$$と$${x_2}$$の２つであり，$${x_1}$$の偏回帰係数を求める場合で言えば，$${x_2}$$から$${x_1}$$を予測する単回帰分析を行ないます。そして，この回帰分析における各対象の予測の誤差を求め，これを新たな説明変数，基準変数を（そのまま）基準変数とした単回帰分析を行ないます。これは，上記の例で言えば，「$${x_1-\hat{x}_{1/2}}$$（$${\hat{x}_{1/2}}$$ は，$${x_2}$$から$${x_1}$$を予測する際の予測値）を説明変数，$${y}$$を基準変数とする単回帰分析を行なう」ということであり，その際の回帰係数が（重回帰分析における）$${x_1}$$の偏回帰係数になります（以上の算出過程と算出結果については，表３の下側および図５，図６を参照してください）。

なお，説明変数同士の中での回帰分析だけでなく，当該の説明変数以外の説明変数から基準変数を予測する回帰分析も最初に行ない，前者の（説明変数同士の中での）回帰分析における予測の誤差を説明変数，後者の回帰分析における予測の誤差を基準変数とした単回帰分析を行なっても，算出される回帰係数の値（すなわち，偏回帰係数の値）は同じ値になります（これは，これまでと同様の場合で言えば，「$${x_1-\hat{x}_{1/2}}$$を説明変数，$${y-\hat{y}_{/2}}$$を基準変数とする単回帰分析を行なったときの回帰係数も説明変数$${x_1}$$の偏回帰係数である$${b_1}$$になる」ということです）。ただし，筆者は，そうなることは知っていても，「なぜそうなるのか」について（現時点では）説明することができません。すみません。[7]

　それから，「まず当該の説明変数以外の説明変数から基準変数を予測する回帰分析を最初に行ない，それにおける予測の誤差を基準変数，当該の説明変数（そのもの）を説明変数とする単回帰分析を行なったときの回帰係数が偏回帰係数である（これまでと同様の場合で言えば，$${x_1}$$を説明変数，$${y-\hat{y}_{/2}}$$を基準変数とする単回帰分析における回帰係数が$${x_1}$$の偏回帰係数である）」と捉えていると受け取れる記述をしている統計書があります。また，（統計学に関して数理的なことを含めてかなりの学びをしたと思われる方から）このような理解をしていると推察される発言を聞いたこともあります。誤解です。ご留意ください。

　以上のように，重回帰分析における各説明変数の偏回帰係数は，それぞれの説明変数そのものと基準変数の関係を表わすものではなく，他の説明変数から当該の説明変数を予測する際の予測の誤差と基準変数の関係を表わしているものです。したがって，先に説明した「予測の誤差という変数の意味」を踏まえるならば，偏回帰係数は，以下のような意味を持つものであることになります。

　まず，予測の誤差は，「各対象の予測される側の変数の値が，予測する側の変数の値$${\underline{\textrm{のわりに}}}$$どの程度大きい（または，小さい）か」を表わしているものでした。ですから，偏回帰係数は，各説明変数そのものの基準変数との関わりの様相を示しているものではなく，「他の説明変数の値$${\underline{\textbf{\textrm{のわりに}}}}$$当該の説明変数の値がどの程度大きい（または，小さい）か」という変数の基準変数との関わりの様相を示しているものであることになります。

　ここで，表３のデータ例における説明変数$${x_1}$$が種々のパソコンの性能で，$${x_2}$$がそれらのパソコンの価格，基準変数$${y}$$が（パソコンを購入しようと思っているある人物の）それぞれのパソコンに対する購入意思の強さだとします。そうすると，この場合の偏回帰係数$${b_1}$$は，「各パソコンの性能そのもの」（より詳しく言えば，「価格を含む他の特性のことを度外視した，各パソコンの性能の良さ」）と「各パソコンに対する購入意思の強さ」の関係を表わすものではなく，「各パソコンが価格のわりにどの程度性能が良い（または，悪い）かということ」と「各パソコンに対する購入意思の強さ」の関係を表わすものであることになります。そして，表３に例示したデータでは，$${x_1}$$のみを説明変数とした単回帰分析および$${x_1}$$と$${x_2}$$を説明変数として同時に組み入れた重回帰分析の結果から，$${x_1}$$単独では（言い換えれば，各パソコンの価格を踏まえないと）「（非常に弱い関係ではあるものの）性能が良いパソコンほど購入意思が弱い」という傾向が認められることになるけれども，各パソコンの価格を踏まえ，「各パソコンが価格のわりにどの程度性能が良い（または，悪い）ものであるか」という捉え方をすると，「（価格のわりに）性能が良いパソコンほど購入意思が強い」という（逆の）傾向が顕著に認められることになります（このことの解釈ないし説明については，後述します）。

　次に，予測の誤差は，「予測する側の変数の値を一定に統制したときの（言い換えれば，各対象の予測する側の変数の値に応じた違いを補正したときの）予測される側の変数の値」と言えるものでした。ですから，偏回帰係数の値は，「当該の説明変数以外の説明変数の値を一定に統制したうえで当該の説明変数の値によって基準変数の値を予測ないし説明しようとしたときに，当該の説明変数の値が１大きくなると基準変数の値が（平均的に）いくら大きくなる（または，小さくなる）か」を表わしていることになります。また，特定の方向の因果関係を示唆する表現を避けるならば，「（当該の説明変数以外の説明変数の値を一定に統制したときの）当該の説明変数の値における１の差異が基準変数の値におけるいくらの差異と（平均的に）対応しているか」を表わしているものであることになります。[8]

　以上のように，偏回帰係数の値は，「$${\underline{\textbf{\textrm{他の説明変数の値が変わらずに}}}}$$当該の説明変数の値のみが１変化したときに，それに対応して基準変数の値が（平均的に）いくら変化しているか」を表わしています。しかし，現実の多くにおいては説明変数同士は無相関ではなく，当該の説明変数の値が変化すれば他の説明変数の値も変化します（たとえば，パソコンの購入の例で言えば，現実には性能の良さが高くなれば価格もそれに応じて高くなります）。[9] そして，偏回帰係数の値は，後者のような「観察された現実の状況下での各説明変数と基準変数の関係」を示しているものではなく，上記のように，あくまで「$${\underline{\textbf{\textrm{他の説明変数の値が変わらずに}}}}$$当該の説明変数の値のみが１変化したとすれば，どうなるか」を示しているものです（２つ前の段落の最後に「後述します」と記した後掲の説明は，以上のことについての具体例に沿った再説明でもあります）。[10]

　最後に，予測の誤差は，「（$${y}$$から$${x}$$によって説明できる部分を取り除いた）$${y}$$の中の$${x}$$とは関係していない成分」を表わしているものでした。ですから，偏回帰係数の値は，他の説明変数からは説明できない，他の説明変数とは関係していない当該の説明変数の（独自の）成分と基準変数の関係を表わすものであることになります。そして，このことから，筆者は，偏回帰係数の解釈に関する記述をする際には，「単独の関わり（ないし，影響）」ではなく，「独自の関わり（ないし，影響）」などと記した方が適切だと思っています。

標準偏回帰係数

　通常は，説明変数によって尺度の単位が異なります。また，変数が異なれば，それぞれを測定する際の手続きないし基準が異なるのであり，「異なる変数の値は異なる尺度上の値である」などと言うこともできるでしょう。当然のことであり，このようなことから，値が１大きくなる（ないし，１異なる）ことの意味が説明変数によって異なっており，「（他の説明変数の値を一定に統制したときに）当該の説明変数の値が１大きくなると基準変数の値が（平均的に）いくら大きくなる（または，小さくなる）か」を表わすものである偏回帰係数の値を説明変数間で比較することができないと考えられる場合がほとんどであることになります。

　たとえば，説明変数$${x_1}$$が野球のピッチャーのkg単位の体重，$${x_2}$$がcm単位の身長で，基準変数$${y}$$が km/時 単位の球速（投げることができる球の速さ）である場合，「体重が１kg変化する（ないし，選手によって１kg異なる）と球速がどのくらい変化する（ないし，異なる）ことになるか」ということと「身長が１cm変化する（ないし，選手によって１cm異なる）と球速がどのくらい変化する（ないし，異なる）ことになるか」ということを比較することには意味がないと考えられます（同じ１という差の値であっても，「１kgの１」と「１cmの１」では同じ意味を持っているとは言えず，そもそもこれらの差の値を比べることがナンセンスだと考えられるからです）。また，体重と身長の各々をどのような単位で表わすか（たとえば，身長をcm単位で表わすかm単位で表わすか）によっても偏回帰係数の値は変わってしまいます。さらに，偏回帰係数の値は各変数の標準偏差（すなわち，得られたデータの散らばりの大きさ）によっても左右されます。

　そこで登場するのが，一般に$${z}$$という記号で表記されている，標準得点とか$${z}$$得点と呼ばれる値です。標準得点は，「個々の測定値の平均値からの偏差（平均値から離れている程度）の$${\underline{\textsf{標準的な値}}}$$」として（変数ごとに）データ全体で１つの値が示される標準偏差とは異なり，各対象の測定値に応じて対象ごとに算出される値であり，対象$${i}$$の変数$${y}$$の測定値を$${y_i}$$，変数$${y}$$について得られたデータの平均値を$${\bar{y}}$$，標準偏差を$${s_y}$$と表わすと，

$$
z_i=\dfrac{y_i-\bar{y}}{s_y}
$$

という式によって算出されます（$${y_i}$$の値は，測定された，素のままの値であることから，標準得点が算出される文脈では，多くの場合，素点と言います）。そして，式が意味することを言葉で表わすと，標準得点は，「各対象の測定値が，平均値に比べて，標準偏差の何倍（言い換えれば，標準偏差の値のいくつ分）大きい（または，小さい）値であるか」ということを示しており，測定値が平均値よりも大きな値であるときは正の値，小さな値であるときは負の値になるとともに，分布の中心に位置する値である平均値から大きく離れた（分布の端の方に位置する）値であるほど，離れている方向が大きい側であれ小さい側であれ，絶対値が大きくなります。すなわち，標準得点は，素点の平均値と標準偏差の値にかかわらず，「各対象の測定値が，得られたデータの分布全体の中で，中心から見て，どちらの方向にどの程度離れたところに位置しているか」という，「各対象の値の分布全体における相対的位置を表わしている指標である」と言えるものです。

　さて，本稿の本題から外れるので詳しい説明は省略しますが，図７に示したように，標準得点は，測定値（素点）が平均値と同じ値である場合を０，測定値における標準偏差１つ分の差の値を１とした尺度上での各対象の値と言えるものであり，標準得点の平均値$${\bar{z}}$$は０，標準偏差$${s_z}$$ は１になります。[11] すなわち，「素点を標準得点に変換すると，変換前の値にかかわらず，標準偏差は必ず１になる」ということであり，身長の測定値がcm単位で表わされていてもm単位で表わされていても，各対象の標準得点の値は変わらないとともに，それらの標準得点の標準偏差は１になります。そして，以上のことに基づいて，多くの（心理学的）研究においては，基準変数も含めた全ての変数の値を標準得点に変換してから分析を行なって，その結果算出される偏回帰係数を基準変数の値を予測または説明する際の各説明変数の規定力（ないし，各説明変数の基準変数との関わりの強さ）の指標としており，このようにして算出される偏回帰係数は，標準偏回帰係数ないし標準化偏回帰係数と呼ばれています。[12]

　上記のように，標準得点の標準偏差は１です。ですから，各説明変数において変換前の値の標準偏差がいくらであっても，変換前の値における１標準偏差分の変化（ないし，差異）が変換後においては“１”という（差の）値で表わされることになります。したがって，標準偏回帰係数は，「当該の説明変数の値がその標準偏差の値分大きくなったときに，基準変数の値がその標準偏差の何倍（平均的に）大きくなる（または，小さくなる）か」を表わしていることになります（ただし，先にも記したように，これは，あくまで他の説明変数の値が一定である場合に関することです）。

　なお，説明変数同士が全て無相関である場合，各説明変数の標準偏回帰係数の値は，その説明変数と基準変数の単相関係数の値と一致します。また，同時に分析に組み入れた複数の説明変数を総合して基準変数の値を予測ないし説明しようとする際の（全体としての）予測の精度（ないし，説明力）に関わる値である重相関係数の２乗は，説明変数同士が全て無相関である場合，各説明変数と基準変数の単相関係数の２乗和になります（これらのことの説明については，吉田，2018bの72～78ページ，および，95～97ページを参照してください）。ですから，説明変数同士が無相関である場合には，重回帰分析を行なう意味ないし必要性はないことになります。

　それから，標準偏回帰係数の絶対値は（相関係数とは異なり）１よりも大きくなることがあり，特に，説明変数同士の相関係数の絶対値が１に近い，かなり大きな値であるときには，このようなことが多々生じます（このようになるデータの具体例については，吉田，2018bの97～101ページ，および，111～112ページを参照してください）。「標準偏回帰係数の絶対値は１を超えない」といった誤った記述をしている統計書があるので，あえて記しました。

脚注

1. 　本来，各変数の値は整数値のみをとる離散変数であるとは限りませんが，説明の便宜上，ここでは整数値のみをとるものとします。

2.  　近年多用されるようになった「交互作用効果の項を組み入れた重回帰分析」においてはこのことは当てはまりません。この「交互作用効果の項を組み入れた重回帰分析」という分析がどのようなことを想定したものであるかや，それにおける（交互作用効果の項の）偏回帰係数の意味などについては，吉田（2018b）の104～110ページを参照してください。

3.  　もちろん，以上のことは，$${x_1}$$ と$${x_2}$$ を入れ替えても同様です。

4.  　$${b_1}$$，$${b_2}$$（および，切片$${a}$$）の実際の求め方の論理については，吉田（2018b）の67ページを参照してください。

5. 　$${z=x^2+xy-2y}$$などというように，ある１つの変数が２つ以上の変数の関数として表わされているケースにおいて，後者の複数の変数の中の１つの変数（たとえば，上記の式における$${x}$$）のみに注目し，他の変数（上記の式における$${y}$$）を定数だと見なして行なわれる微分を偏微分と言います。この偏微分という言葉における「偏」という漢字の適用と偏回帰係数という言葉における「偏」という漢字の適用は通底しているものだと考えられるとともに，いずれもpartialという英語の訳語だと思いますが，筆者は，「他の変数を一定にする」という文脈を表わす訳語としてなぜ「偏」という言葉が使われるようになったのかについて，推察できないとともに，違和感を覚えています（筆者がどうこう言っても仕方がないであろう余談です：すみません）。

6. 　単回帰分析においては，回帰係数と相関係数の間に「回帰係数$${=}$$相関係数$${\times}$$（基準変数の標準偏差$${\div}$$説明変数の標準偏差）」という関係があり，標準偏差は負の値になることはないので，回帰係数の符号と相関係数の符号は必ず一致します。
   　なお，１の位の０という数値を相関係数の場合には省略して表記し，回帰係数の場合には省略していませんが，これは，相関係数は絶対値が１を超えない値であるのに対して，回帰係数は１を超え得る値であることによります。

7. 　「だったら読者を混乱させるようなことをわざわざ書くな」などとお叱りを受けそうですが，次の段落に記すこととの関係で，あえて記しました。

8. 　回帰係数という項の第１段落の最後に「この段落に記したことは，$${\underline{\textrm{基本的には}}}$$，本稿の主たる説明対象である偏回帰係数についても該当します」と記しましたが，それは，「偏回帰係数の場合には“当該の説明変数以外の説明変数の値を一定に統制したときの”という断り書きが付くということ以外は，重回帰分析における偏回帰係数は単回帰分析における回帰係数と同じ意味を持つものである」という意味です。

9. 　表３のデータもそのようにしてあり，性能$${x_1}$$と価格$${x_2}$$の相関は .97になります（説明の便宜のために，あえて，このような極端な値になるようにしてあります）。

10. 　このような意味では，当該の説明変数のみを用いた単回帰分析の結果や当該の説明変数と基準変数の（他の変数のことを考慮しない，通常の相関係数である）単相関係数よりも，偏回帰係数の方が，「当該の説明変数$${\underline{\textrm{そのもの}}}$$と基準変数の関係の様相を表わしている」という言葉が当てはまるようにも思えます。曖昧なことで，すみません。

11. 　このことについての詳しい説明は，吉田（1998）の129～133ページ，および，吉田（2018a）の101～104ページを参照してください。また，標準得点の意味についての理解を深めるためには，標準偏差に関して，単に「測定値の散らばりの程度である散布度の指標」というように捉えるだけでなく，「標準偏差の値が，データの分布の様相を表わす度数ポリゴン（度数分布多角形）のような図において，どの部分（の間隔）に対応しているものか」ということを理解しておく必要があります。このことについては，吉田（1998）の56～59ページ，および，吉田（2018a）の11～12ページを参照してください。

12. 　ただし，当然のことながら，「体重が１kg異なる（ないし，変化する）と球速がどの程度異なる（ないし，変化する）か」や「身長が１cm異なる（ないし，変化する）と球速がどの程度異なる（ないし，変化する）か」という具体的なことについて推定したい場合には，標準偏回帰係数ではなく，偏回帰係数に注目すべきだと思います。

引用文献

• 吉田 寿夫 (1998). 本当にわかりやすい すごく大切なことが書いてある ごく初歩の統計の本　北大路書房

• 吉田 寿夫 (2018a). 本当にわかりやすい すごく大切なことが書いてある ごく初歩の統計の本 補足Ⅰ　北大路書房

• 吉田 寿夫 (2018b). 本当にわかりやすい すごく大切なことが書いてある ちょっと進んだ 心に関わる 統計的研究法の本Ⅲ　北大路書房

執筆者プロフィール

他の回はこちら：