説明・因果関係の探究における標準偏回帰係数の意味[1]

　先に記したように，実際に報告されている（心理学的）研究においては，重回帰分析は，説明ないし因果関係の探究のために用いられています。そして，各説明変数の基準変数に対する因果効果（前者が大きくなるにつれて後者も大きくなるか，前者が大きくなるにつれて後者は小さくなるかという意味での影響の方向と，その影響の強さ）に関しては，通常，標準偏回帰係数に基づいて考察がなされています。しかし，林・黒木（2016）や狩野（2002），Pedhazur（1997）などが論じているように，各説明変数（および，後述する統制変数）の間に想定される因果関係によって，標準偏回帰係数の値の意味（ないし，標準偏回帰係数に基づいて検討を行なうことの適切さ）は異なります。そこで，ここでは，ある説明変数（$${\hspace{-.5pt}x_1 \hspace{-.5pt}}$$）の基準変数（$${\hspace{-.5pt}y \hspace{-.5pt}}$$）に対する因果効果について検討する際の標準偏回帰係数の意味について，「分析に投入する諸変数間の因果関係における他の説明変数（$${\hspace{-.5pt}x_2 \hspace{-.5pt}}$$）の位置づけ」という点から分けた基本的な２つの場合に関して説明します。なお，実際にはそうとは限りませんが，直接的な影響であれ，第３の変数に媒介された間接的な影響であれ，$${x_1}$$ と$${y}$$の間の因果の方向は$${x_1\rightarrow y}$$（のみ）であるものとします。

他の説明変数が交絡変数である場合

　まず１つ目は，他の説明変数が$${x_1\rightarrow y}$$という因果関係によって示されるはずの関係を攪乱している，交絡変数などと呼ばれるものである場合です。

　ここで，交絡というのは，ある変数$${\textbf{\textit{y}}}$$の状態（値）に影響を及ぼす複数の原因の候補が交わり絡み合っているために$${\textbf{\textit{y}}}$$の値の変動（対象や条件の間の違い）の原因が特定できなくなっている状態のことであり，変数間の因果関係を明らかにしようとしている研究にとって非常に望ましくないと言えるものです。基本的な場合でもう少し詳しく説明すると，$${y}$$の値に影響を及ぼし得る２つの変数（$${\hspace{-.5pt}x_1 \hspace{-.5pt}}$$，$${\hspace{-.5pt}x_2 \hspace{-.5pt}}$$）の間になんらかの関係がある（すなわち，一方の変数の値によって他方の変数の値が異なっている）と，各対象の$${x_1}$$の値（ないし，$${x_1}$$に関する条件）によって$${y}$$の値が異なることが示されても，そのような「$${y}$$の値の対象（ないし，条件）間の違い」は$${x_1}$$の値が対象ないし条件によって異なっているからではなく，それと連動して異なっている$${x_2}$$の値の対象（ないし，条件）間の違いによるのかもしれないことになってしまいます。ですから，$${y}$$の値が対象や条件によって異なっている原因に関して明確な判断を下すことが困難になり，このような状態のことを交絡と呼んでいます。

　具体例の１つは，先に提示した「家の工法」と「家が地震によって倒壊したか否か」に関するものであり，工法と（この場合の交絡変数である）築年の間に関係がある（すなわち，工法によって築年が異なっている）ため，２×４工法という新しい工法で建てられた家の方が既存の工法で建てられた家よりも倒壊率が低くても，それは，２×４工法という工法で建てられた家の方が築年の値が全般に小さい（新しい家である）からかもしれません。そして，そうであれば（すなわち，本当は工法は倒壊するか否かに影響を及ぼしていないとすれば），「２×４工法という新しい工法で建てられた家の方が既存の工法で建てられた家よりも倒壊率が低い」という，工法と倒壊したか否かという変数の間に示された関係は，「両者の間の因果関係によるものではない」という意味で本来のものではないことになり，このようなことから，以上のようなことによって示される相関は擬似相関と呼ばれています。

　さて，築年の値が大きければ（すなわち，その家がかなり前に建てられたものであれば），２×４工法という新しい工法はまだ開発されていないので，２×４工法の家であることはないはずです。そして，築年の値が小さい，最近建てられた家であるほど，２×４工法で建てられたものである率が高いと考えられます。すなわち，「いつ建てられた家であるか」とも言える変数である築年は，用いられた工法を左右することになります。一方，どんな工法で建てられた家も年月が経つにつれて築年の値が大きくなるのですから，工法によって築年が異なっていても，工法が築年に影響を及ぼすことはないはずです（ただし，「ある工法で建てられた家は傷んだり壊れたりしやすいために築年の値が大きいものがほとんど存在しないので，工法によって築年が違ってくる」というようなことはあり得るかもしれません）。ですから，築年と工法の因果関係の方向は，「築年$${\rightarrow}$$工法」（のみ）だと考えていいと思います。また，築年の値が大きい（すなわち，建てられてから年月が経っている）家ほど種々の箇所にガタが来ている可能性が高くなると考えると，築年は倒壊するか否かに影響を及ぼし得ると言えるでしょう。一方，「倒壊すると築年が増える」などということは考えられないので，「倒壊したか否かが築年に影響を及ぼす」という方向の因果関係はあり得ないでしょう。したがって，築年と倒壊したか否かの因果関係の方向は，「築年$${\rightarrow}$$倒壊したか否か」（のみ）だと考えていいと思います。そして，これらに加えて，工法が倒壊したか否かに影響を与えているならば，工法（$${\hspace{-.5pt} x_1\hspace{-.5pt}}$$），築年（$${\hspace{-.5pt}x_2 \hspace{-.5pt}}$$），倒壊したか否か（$${\hspace{-.5pt}y \hspace{-.5pt}}$$）という３つの変数の間の因果関係は，図８に示したようになると考えられます。

　ここで，図８に示したような因果関係についての想定（因果モデル）のもとで考えると，先に記したこの例における擬似相関は，$${x_2}$$の値が対象によって変化する（ないし，異なる）ことによって$${x_1}$$の値と$${y}$$の値の双方が変化する（ないし，対象によって異なるようになる）ことによるものであることになります。そして，そうであるならば，$${x_2}$$を変動させなければ（すなわち，一定にすれば）擬似相関は生じなくなり，$${x_1}$$と$${y}$$の単相関が示している両者の関係から$${x_2}$$が介在した擬似相関である部分が取り除かれて，$${x_1}$$の$${y}$$に及ぼす影響を意味するものである「$${x_1}$$の$${y}$$に対する因果効果」が析出されることになります。以上のことから，「$${\textbf{\textit{x}}_\textbf{1}}$$の$${\textbf{\textit{y}}}$$に対する因果効果を捉えることが目的であるならば，$${\textbf{\textit{x}}_\textbf{1}}$$と$${\textbf{\textit{y}}}$$の関係を攪乱する交絡変数である$${\textbf{\textit{x}}_\textbf{2}}$$は，$${\textbf{\textit{x}}_\textbf{1}}$$とともに説明変数の１つとして分析に組み入れる必要がある」ことになります（このような「本来，基準変数に及ぼす効果について検討する対象ではないが，主たる説明変数が基準変数に及ぼす効果について検討する際に考慮する必要があると考えられるために分析に組み入れる変数」は，説明変数ではなく，統制変数と呼ばれることもあります）。

　なお，上記の擬似相関についての説明は，もっとも基本的なケースを取り上げたものであり，次に例示するように，$${x_1}$$と$${x_2}$$の間にはいずれの方向の因果関係も存在していないけれども，第４の変数$${x_3}$$が$${x_1}$$と$${x_2}$$の双方に影響を及ぼしているために$${x_1}$$と$${x_2}$$の間に関係（交絡）が生じ，かつ，上記と同様$${x_2}$$が$${y}$$に影響を及ぼすために，$${x_1}$$と$${y}$$の間に（$${x_1 \rightarrow y}$$という因果関係は存在していないにもかかわらず）相関が示される（すなわち，擬似相関が発生する）などというようなケースもあり得ます。そして，このようなことも含めて，擬似相関を（筆者なりに）もっと一般的に定義すると，「擬似相関とは，$${\textbf{\textit{x}} \rightarrow \textbf{\textit{y}}}$$もしくは$${\textbf{\textit{y}} \rightarrow \textbf{\textit{x}}}$$という直接的なものであれ，$${\textbf{\textit{x}} \rightarrow \textbf{\textit{z}} \rightarrow \textbf{\textit{y}}}$$もしくは $${\textbf{\textit{y}} \rightarrow \textbf{\textit{z}} \rightarrow \textbf{\textit{x}}}$$などというような第３の変数$${\textbf{\textit{z}}}$$に媒介された間接的なものであれ，当該の２変数の一方から他方に向かうパス（直接的な影響ないし影響の連鎖）がまったく存在していないにもかかわらず示される（$${\hspace{-.5pt} \textbf{\textit{x}}}$$と$${\textbf{\textit{y}}}$$の間の）相関である」ということになります。

　$${x_2}$$が交絡変数である例を，もう１つ提示します。上記の例では，「$${x_1 \rightarrow y}$$という，$${x_1}$$の$${y}$$に対する直接的な効果によって生じる関係」と「$${x_1 \leftarrow x_2 \rightarrow y}$$という，$${x_2}$$が$${x_1}$$と$${y}$$の双方に影響を及ぼすことによって生じる関係」のどちらも（「２×４工法という新しい工法で建てられた家の方が既存の工法で建てられた家よりも倒壊率が低い」という）同じ様相のものでした。それに対して，今度は，$${\textbf{\textit{x}}_\textbf{1} \rightarrow \textbf{\textit{y}}}$$と$${\textbf{\textit{x}}_\textbf{1} \leftarrow \textbf{\textit{x}}_\textbf{2} \rightarrow \textbf{\textit{y}}}$$が逆の現象を生じさせるものであるために，それらが相殺し合って単相関では$${\textbf{\textit{x}}_\textbf{1}}$$と$${\textbf{\textit{y}}}$$の間に関係が示されないケースであり，このような場合の無相関を擬似無相関と言います。「偏回帰係数という値の意味」という項で提示したパソコンの購入に関わる例，および，一番最初の「２つの変数の関係について検討する際に他の変数を一定に統制することの必要性」という項で提示した学習方略の使用に関わる例が該当例であり，ここでは前者で説明します。

　まず，各パソコンの性能$${x_1}$$の購入意思$${y}$$に対する直接的な影響である $${x_1 \rightarrow y}$$という効果です。常識的に考えるならば，この効果は「性能が良いので購入したくなる」というものであり，この効果しか存在していなければ，性能の良さと購入意思の強さの間には正の相関関係が生じるはずです。しかし，性能$${x_1}$$と価格$${x_2}$$の間には「性能が良いほど価格が高い」という正の相関関係が存在するとともに，価格$${x_2}$$は購入意思$${y}$$に対して「価格が高いので購入したくなくなる」という影響を及ぼすものと考えられます。そして，性能と価格の間の正の相関は，生産コストという第４の変数（$${\hspace{-.5pt} x_3 \hspace{-.5pt}}$$）が介在した擬似相関であるとします。すなわち，「“（仕入れ価格が高い）良質な材料を使って入念かつ精巧に作られた（生産コストが高い）ものであるために，性能が良くなるとともに，採算をとるために価格を高くした”ことによって，上記のような“性能が良いほど価格が高い”という正の相関関係が生じる」ということです。なお，「生産コストがどうであれ，性能が良い製品が出来たので価格を高くした」ということもあり得ると思いますが，説明の便宜上，ここでは，性能と価格の関係は生産コストが介在した擬似相関（のみによるもの）だと考えることにします（少なくとも，「価格が高いものほど性能が良い」という関係は存在しても，「価格が高いので性能が良くなる」わけではないはずです）。

　以上の因果関係を示したものが図９であり，この因果モデルのもとで考えると，まず，生産コストが高いほど，性能が良くなります。また，生産コストが高いほど，価格を高くせざるを得なくなり，価格が高くなるほど，購入意思は弱くなります。したがって，生産コスト（の変動）を出発点とする以上のような影響により，他の効果がなければ，性能と購入意思の間には「性能が良いものほど購入意思が弱い」という負の擬似相関が生じます。しかし，「他の効果はない」のではなく，先に記した「正の相関関係を生じさせる直接効果」が存在しており，「これが負の擬似相関を生じさせる効果と相殺し合って，単相関が無相関になる」と考えられます。そして，以上のようなことになっているならば，生産コストまたはそれによって変動している価格を変動させなければ（すなわち，一定にすれば）擬似相関は生じなくなり，$${x_1}$$と$${y}$$の単相関が示している両者の関係から$${x_3}$$ないし$${x_2}$$が介在した擬似相関である部分が取り除かれて，$${x_1}$$の$${y}$$に対する因果効果が析出されることになります。以上のことからも，「$${\hspace{-.5pt} \textbf{\textit{x}}_\textbf{1}}$$の$${\textbf{\textit{y}}}$$に対する因果効果を捉えることが目的であるならば，$${\textbf{\textit{x}}_\textbf{1}}$$と$${\textbf{\textit{y}}}$$の関係を攪乱する交絡変数である$${\textbf{\textit{x}}_\textbf{2}}$$（ないし，$${\hspace{-.5pt} \textbf{\textit{x}}_\textbf{3} \hspace{-.5pt}}$$）は，$${\hspace{-.5pt} \textbf{\textit{x}}_\textbf{1}}$$とともに説明変数の１つとして分析に組み入れる必要がある」ことになります。

　以上を要約すると，「説明変数（ないし，統制変数）$${\hspace{-.5pt} \textbf{\textit{x}}_\textbf{2}}$$が交絡変数である場合，説明変数$${\textbf{\textit{x}}_\textbf{1}}$$と基準変数$${\textbf{\textit{y}}}$$の単相関係数は，$${\hspace{-.5pt} \textbf{\textit{x}}_\textbf{1} \rightarrow \textbf{\textit{y}}}$$という（本来見いだすべき）効果のみを反映したものではなく，$${\hspace{-.5pt} \textbf{\textit{x}}_\textbf{1} \leftarrow \textbf{\textit{x}}_\textbf{2} \rightarrow \textbf{\textit{y}}}$$などという，$${\textbf{\textit{x}}_\textbf{2}}$$の介在によって生じる擬似的な効果も含むものとなってしまう」のに対して，「この場合の（$${\hspace{-.5pt} x_2}$$を一定に統制した）$${\hspace{-.5pt} x_1}$$の標準偏回帰係数は，$${x_1 \rightarrow y}$$の効果のみを反映したものになる」ので，「$${\hspace{-.5pt} \textbf{\textit{x}}_\textbf{1}}$$の$${\textbf{\textit{y}}}$$に対する因果効果を捉えることが目的であるならば，交絡変数は，全て（現実には，できる限り）分析に組み入れなければならない」ということになります。

他の説明変数が媒介変数である場合

　今度は，分析に投入する諸変数間の因果関係における$${x_2}$$の位置づけが，$${x_1 \leftarrow x_2 \rightarrow y}$$などというような，擬似相関や擬似無相関の発生につながる交絡変数である場合ではなく，$${x_1 \rightarrow x_2 \rightarrow y}$$などというような，説明変数$${x_1}$$が基準変数$${y}$$に影響を及ぼす過程に介在している媒介変数である場合です（$${\hspace{-.5pt} x_1}$$と$${x_2}$$の間の矢印の向きの違いに注目してください）。

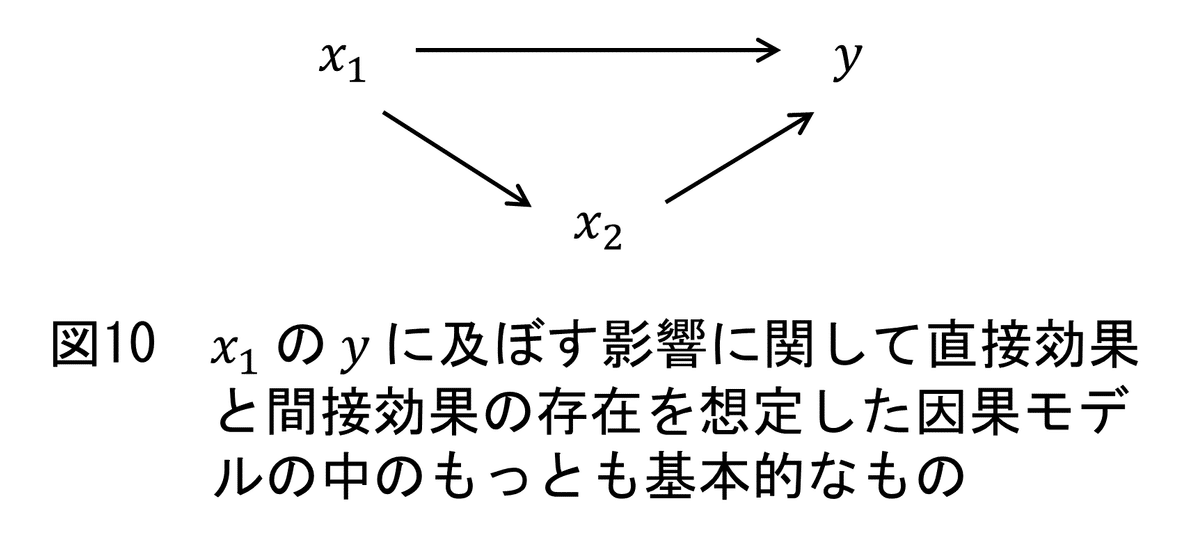
　図10に示した因果モデルはこのような場合のもっとも基本的なものであり，この因果モデルにおける$${x_1 \rightarrow x_2 \rightarrow y}$$という因果連鎖による効果は，直接的なものではなくても，$${x_1}$$における変化ないし差異が$${y}$$に変化ないし差異をもたらす（すなわち，$${x_1}$$が$${y}$$に影響を及ぼす）ことを意味するものなのですから，$${\hspace{-.5pt} x_1}$$の$${y}$$に対する因果効果の一部であることになります。ですから，この因果モデルのもとでの$${x_1}$$の$${y}$$に対する因果効果は，「$${\hspace{-.5pt} x_1 \rightarrow y}$$という直接効果」と「$${\hspace{-.5pt} x_1 \rightarrow x_2 \rightarrow y}$$という，$${\hspace{-.5pt} x_2}$$に媒介された間接効果」の和であることになり，$${\hspace{-.5pt} x_1}$$と$${y}$$の単相関係数は，この「$${x_1}$$の$${y}$$に対する（全体的な）因果効果の様相」を表わしています。これに対して，$${x_2}$$を説明変数の１つないし統制変数として組み入れた重回帰分析における$${x_1}$$の標準偏回帰係数は，$${\hspace{-.5pt}x_2}$$を一定にした（すなわち，$${\hspace{-.5pt}x_2}$$の変動をなくした）ときの$${x_1}$$と$${y}$$の関係を表わすものなのですから，「$${x_2}$$の変動に媒介されて$${y}$$が変動する」という間接的な因果効果によって生じる関係を取り除いた，直接効果のみを反映したものになります（「$${\hspace{-.5pt}x_1}$$の中の$${x_2}$$とは関係していない成分の$${y}$$に及ぼす効果のみを反映したものになる」などと記述することもできると思います）。そして，以上のことから，「$${\hspace{-.5pt} \textbf{\textit{x}}_\textbf{1}}$$の$${\textbf{\textit{y}}}$$に対する（$${\hspace{-.5pt} \textbf{\textit{x}}_\textbf{2}}$$と関係している部分も含めた，全体的な）因果効果を捉えることが目的であるならば，$${\textbf{\textit{x}}_\textbf{1}}$$が$${\textbf{\textit{y}}}$$に影響を及ぼす過程に介在している媒介変数である$${\textbf{\textit{x}}_\textbf{2}}$$は，分析に組み入れてはならない」ことになります。

　ここで，媒介変数だと想定している変数を組み入れた重回帰分析を行なっている研究の具体例を１つ提示します。『美人ステレオタイプは存在するか』というタイトルの論文（垣内，1996）であり，「美人は性格が良い」という，美人ステレオタイプと呼ばれている現象に関するものです。筆者は，この研究を，主に「コストのかかることをていねいに行なっている」という点から基本的には高く評価していますが，「示された結果を（最終的に）どう捉え・記述するか」という点に関して大きな問題を有しているとも思っています。どういうことなのか，以下に詳しく説明します。[2]

　垣内（1996）では，「美人である（と思う）ことが性格が良い（望ましい）と思うことにつながる」ということが想定されています。ですから，「美人だと思う程度」が「性格が望ましいと思う程度」に及ぼす影響を問題にしているものであることになり，前者が$${x_1}$$，後者が$${y}$$，であることになるでしょう。そして，垣内（1996）では，このような影響が生じる過程に好意度という変数が媒介変数として介在していることを想定しています。すなわち，「美人だと思うこと」が直接「性格が望ましいと思うこと」につながるのではなく，前者が後者に及ぼす影響は，「美人やなあ$${\rightarrow}$$好っきやわあ（クラクラ）$${\rightarrow}$$ええ子やなあ」という間接的な因果関係によって生じていると考えています（おちゃらけた記述で，すみません）。ですから，ここでは，媒介変数として想定されている好意度が$${x_2}$$であることになり，このような「好意度に媒介された，$${x_1 \rightarrow x_2 \rightarrow y}$$という間接効果」に加えて「$${x_1 \rightarrow y}$$という直接効果」の存在も想定するならば，垣内（1996）には明示されていませんが，図11に示した因果モデルが想定されていることになるでしょう。[3]

　さて，図11に示した因果モデルのもとでは，先に説明したように，$${x_2}$$を説明変数の１つないし統制変数として組み入れた重回帰分析における$${x_1}$$の標準偏回帰係数は$${x_1}$$が$${y}$$に及ぼす直接効果を表わすものであることになりますが，垣内（1996）では，「美人だと思う程度（$${\hspace{-.5pt} x_1 \hspace{-.5pt}}$$）と性格が望ましいと思う程度（$${\hspace{-.5pt} y \hspace{-.5pt}}$$）の単相関係数は正である」，すなわち，「好意度（$${\hspace{-.5pt} x_2 \hspace{-.5pt}}$$）を一定に統制しないと，“美人だと思うほど性格が望ましいと思う”という関係が認められる」のに対して，（好意度を一定に統制したときのものである）美人だと思う程度$${x_1}$$の標準偏回帰係数は０に近い値，もしくは，（“美人だと思うほど性格が望ましくないと思う”という関係であることを意味する）負の値になるという仮説を設定しています。そして，88人の大学生に43人の女性の顔写真を１枚ずつ提示して，$${\hspace{-.5pt} x_1 \hspace{-.5pt}}$$，$${\hspace{-.5pt} x_2 \hspace{-.5pt}}$$，$${\hspace{-.5pt} y}$$の各々に関する評定を求め，これらのデータについて，各変数間の単相関係数の算出や，$${\hspace{-.5pt} x_1}$$と$${x_2}$$を説明変数，$${\hspace{-.5pt} y}$$を基準変数とする重回帰分析などを行なっています。[4]

　結果は，大筋，図12と図13に相関図で例示した仮説通りのものであり，$${\hspace{-.5pt} x_1}$$と$${y}$$の単相関係数は全般に正の値であるのに対して，$${\hspace{-.5pt} x_1}$$の標準偏回帰係数は，性格の側面によって，０に近い値もしくは負の値になりました。そして，このような結果に基づいて，垣内（1996）では，「美人に対して“性格が望ましい”という認知がなされるのは，美人ステレオタイプが共有されているからではなく，ただ単に美人に対して好意を抱く反応傾向が強いためである（筆者なりにもう少し詳しく記述するならば，美人に対しては好意を抱きやすく，その美人であることによって抱かれた好意が性格の望ましさについての認知に影響を及ぼすからである）」とか「性格の側面によっては美人は性格が良くない”という逆美人ステレオタイプが共有されている」といった内容の解釈が行なわれています。

　さあ，このような解釈・記述は妥当でしょうか。

　筆者は，「美人（だと思った人）に対して“性格が望ましい”という認知がなされるのは，美人に対して好意を抱く反応傾向が強いためである」という解釈，すなわち，先におちゃらけた記述をした「“美人だと思う程度”が“性格が望ましいと思う程度”に及ぼす影響過程に好意度が媒介変数として介在している」という解釈は妥当であり，そのような解釈と合致する（「好意度と関係している成分を取り除くと，“美人だと思うほど性格が望ましいと思う”という関係が認められなくなったり，“美人だと思うほど性格が望ましくないと思う”という関係が認められるようになる」という）データを提示していることには意味があると思っています。しかし，好意度に媒介された間接的因果であっても，美人であると思う程度が原因となって性格の望ましさについての認知が左右されていることを想定したものなので，それは「美人であると認知することの効果」の一部分であることになると思います。そして，そうであれば，美人ステレオタイプという概念（および，それに沿った認知）には，このような間接効果によって生じる現象を含めるべきであり，美人だと思う程度が性格が望ましいと思う程度に及ぼす（全体的な）効果（および，それによって生じる現象）についての検討は，（標準）偏回帰係数ではなく，単相関係数に基づいて行なうべきです。すなわち，先に記したように「$${x_1}$$の$${y}$$に対する（全体的な）因果効果を捉えることが目的であるならば，$${\hspace{-.5pt} x_1}$$が$${y}$$に影響を及ぼす過程に介在している媒介変数である$${x_2}$$は，分析に組み入れてはならない」のであり，美人であるということに関わるステレオタイプの内容について検討する際には，（好意度を一定に統制した）美人だと思う程度の標準偏回帰係数ではなく，「美人だと思う程度」と「性格が望ましいと思う程度」の単相関係数に基づけば良いのです。そして，このように考えると，「美人ステレオタイプが共有されていない」とか「“美人は性格が良くない”という逆美人ステレオタイプが共有されている」といった解釈は妥当ではなく，「美人だと思う程度」と「性格が望ましいと思う程度」の単相関係数が正であるならば，それが好意度に媒介されたものであっても，「“美人は性格が良い”というステレオタイプが多くの人に共有されている」と言えるのだと思います。

脚注

1. 　この項に記すことは，標準偏回帰係数だけでなく，関係を検討している主たる対象である２つの変数（$${\hspace{-.5pt} x}$$と$${y \hspace{-.5pt}}$$）の各々を統制変数（$${\hspace{-.5pt} z \hspace{-.5pt}}$$）から予測する際の予測の誤差同士の相関係数である偏相関係数にも該当することです（偏相関係数については，吉田，2018の１章を参照してください）。

2. 　ルッキズムと呼ばれて（これまでよりも大きく）問題視されるようになった事柄に関わる研究であり，このようなことについて検討すること自体に倫理的な面で問題があると思われる方がいるかもしれません。しかし，この研究は，「美人は性格が良い」と思うことを肯定しているものでも否定しているものでもなく（かつ，そのようなことに関する発言をすることを肯定しているものでもなく），「私たちは，なぜそのように思うのか」という心理過程に迫ろうとしているものだと筆者は捉えています。そして，「美人は性格が良い」と思うことの是非はともかくとして，現実に私たち（の多く）にそのように思う傾向があるのならば，「なぜそう思うのか」という，そこに介在する心理過程に関して探究しようとすることは，基本的には問題視されるべきことではないと思っています（ただし，これまた曖昧な記述で申し訳ありませんが，「美人度に関する評定を求めることは，そのようなことに注目して人を評価することを肯定していることになるのではないか」といった批判に対しては，明確に否定することはできないとも思っています）。
   　以上，記すまでもないことだったかもしれませんが，不快になられる方がいるのではないかと懸念し，あえて記させていただきました。

3. 　日常の人間関係においては，「（美人であること以外の原因によって）好意を抱いているために，美人だと思うようになる」といった，$${\hspace{-.5pt} x_2 \rightarrow x_1}$$という方向の因果関係や，「性格が望ましいと思ったので，好意を抱くようになる」といった，$${\hspace{-.5pt} y \rightarrow x_2}$$という方向の因果関係も存在していると思いますが，垣内（1996）では，参加者にとってまったく知らない者であった人物について顔写真のみを提示して各変数に関する評定を求めているので，ここでは上記のような因果関係の存在を想定しなくても良いものと考えます（ただし，「美人だと思う$${\rightarrow}$$性格が望ましいと思う$${\rightarrow}$$好意を抱く」などといった因果関係が存在している可能性を完全に否定することもできないとも思います）。

4. 　垣内（1996）では，このような分析を，各写真の女性に対する88人の参加者の各変数における平均評定値に基づいて行なうとともに，各参加者においても行なっていますが，前者の分析法には，吉田（2018）で論じている「データの集合による相関関係の変化」という問題があります。詳しくは，吉田（2018）の159～165ページを参照してください。

引用文献

• 林 岳彦・黒木 学 (2016). 相関と因果と丸と矢印のはなし ―はじめてのバックドア基準―　岩波データサイエンス刊行委員会（編） 岩波データサイエンス Vol.3（pp.28-48）岩波書店

• 垣内 理希 (1996). 美人ステレオタイプは存在するか　社会心理学研究, 12, 54-63.

• 狩野 裕 (2002). 構造方程式モデリング，因果推論，そして非正規性　竹内 啓・甘利 俊一・狩野 裕・佐藤 俊哉・松山 裕・石黒 真木夫　多変量解析の展開 ―隠れた構造と因果を推理する― (pp.65-129)　岩波書店

• Pedhazur, E.J. (1997). Multiple regression in behavioral research: Explanation and prediction (3th ed.). Fort Worth, Texas: Harcourt Brace College Publishers.

• 吉田 寿夫 (2018). 本当にわかりやすい すごく大切なことが書いてある ちょっと進んだ 心に関わる統計的研究法の本Ⅲ　北大路書房

執筆者プロフィール

他の回はこちら：