1. ベイズで仮説を評価したい！

　「心」というつかみどころのない対象をどうにかして科学的に探究しようとしてきた心理学は，自然科学よろしく，仮説検証のスタイルを採用することで大きく発展してきました。実際，心理学の論文のほとんどは，はじめに理論的な仮説を立てて，次にその仮説から導かれる予測が実際に得られたデータと整合的かどうかを統計的に判断して仮説を評価するという，いわゆる仮説演繹法を採用しているように見えます[1]。

　近年は，伝統的な頻度主義統計学だけでなく，ベイズ統計学を利用したデータ分析も主流になりつつあります。ところが，ベイズ統計学に基づく仮説評価の方法はさまざまで，研究者によって「推し」の方法が異なっていたりと，初学者泣かせな面もあります。また，最も代表的な仮説の評価指標であるベイズファクターでさえ論文中での誤用が多いことが指摘されています (Tendeiro et al., 2024)。こういった現状を踏まえて，本記事ではベイズ統計学を利用した仮説評価の方法について初学者向けに整理と解説を試みることにしました。ここでは伝統的な分類に倣い，仮説評価の方法をモデル比較アプローチ (model-comparison-based approach) とパラメータ推定アプローチ (estimation-based approach) に大別します。本記事では特に，モデル比較アプローチに基づく指標としての周辺尤度およびベイズファクターと，パラメータ推定アプローチに基づく指標の一例としての方向性確率 (probability of direction; pd) を取り上げ，それぞれについて解説していきます。

2. ベイズ統計学のおさらい

　仮説評価の方法を解説する前に，ベイズ統計学の基本を復習しておきましょう。ベイズ統計学は，パラメータの値に関する信念の大きさを確率で表現し，データに基づいてその信念を更新するという考え方に基づいています。ここで，データを観測する前のパラメータ$${\bm \theta}$$の各値に関する信念の大きさを事前分布$${p(\bm \theta)}$$で表します。また，データ$${\bm y}$$を観測して更新されたパラメータ$${\bm \theta}$$の各値に関する信念の大きさを事後分布$${p(\bm \theta \vert \bm y)}$$で表します。事前分布と事後分布の関係は，ベイズの定理より

$$
p(\bm \theta \vert \bm y)=\dfrac{p(\bm y\vert \bm \theta)p(\bm \theta)}{p(\bm y)}
$$

と表せます。右辺の分子にある$${p(\bm y\vert \bm \theta)}$$は尤度関数と呼ばれ，データ$${\bm y}$$がパラメータ$${\bm \theta}$$の各値に対して持つ相対的な証拠の大きさを反映していると解釈することができます。尤度関数がどのような式になるのかは，分析者が想定するデータ生成過程，すなわち確率モデルに依存します[2]。また，右辺の分母にある$${p(\bm y)}$$は周辺尤度と呼ばれ，後述するモデル比較アプローチにおいて特に重要な役割を果たします。

　本記事では分かりやすさのために，対応のない$${t}$$検定に相当する分析を例として取り上げます。具体的には，60人の研究対象者を30人ずつ無作為に統制群と介入群に割り当てたうえで何らかのアウトカムをデータとして収集し，介入による平均因果効果の有無 (アウトカムの平均値差が$${0}$$か否か) を評価するケースを考えます。

3. モデル比較アプローチ：周辺尤度とベイズファクター

　モデル比較アプローチでは，評価したい複数の仮説をそれぞれモデルとして表現し，どのモデルがデータに最も適合しているかを考えます。今回の例では介入の効果の有無に関心があるので，介入の効果が存在すると仮定するモデル$${\mathcal{M}_1}$$(効果ありモデル) と効果が存在しないと仮定するモデル$${\mathcal{M}_0}$$(効果なしモデル) をそれぞれ考えることにしましょう。

　効果ありモデル$${\mathcal{M}_1}$$は，参加者$${i}$$のアウトカムの値を$${y_i}$$と表すと，例えば

$$
y_i \sim \begin{cases}
    \textrm{Normal}\left (\mu-\dfrac{\delta\sigma}{2},\sigma^2\right ) &\text{if } i \text{が統制群} \\
    \textrm{Normal}\left (\mu+\dfrac{\delta\sigma}{2},\sigma^2\right ) &\text{if } i \text{が介入群}
  \end{cases}
$$

と表現することができます[3]。この式は，統制群のアウトカムが平均$${\mu-\dfrac{\delta\sigma}{2}}$$，分散$${\sigma^2}$$の正規分布に従い，介入群のアウトカムが平均$${\mu+\dfrac{\delta\sigma}{2}}$$，分散$${\sigma^2}$$の正規分布に従うという分析者の信念を表したモデルです。このモデルに含まれるパラメータは$${\mu}$$，$${\delta}$$，$${\sigma^2}$$の3つです。$${\delta}$$は平均値の群間差すなわち平均因果効果を標準偏差$${\sigma}$$で標準化したもの (平均値の群間差が標準偏差いくつ分か) であり，今回の分析において最も関心のあるパラメータとなります。パラメータの事後分布は，効果ありモデル$${\mathcal{M}_1}$$が仮定されていることを明示的に書くと，

$$
p(\mu, \delta, \sigma^2\vert \bm y,\mathcal{M}_1 )=\dfrac{p(\bm y\vert \mu, \delta, \sigma^2, \mathcal{M}_1) p(\mu, \delta, \sigma^2 \vert \mathcal{M}_1)}{p(\bm y\vert \mathcal{M}_1)}
$$

と表せます。

　これに対し，介入の効果が存在しないことを仮定する効果なしモデル$${\mathcal{M}_0}$$は，効果ありモデル$${\mathcal{M}_1}$$の$${\delta}$$を$${0}$$に固定することで，

$$
y_i \sim \textrm{Normal}(\mu, \sigma^2)
$$

のように表すことができます。このモデルには，統制群か介入群かにかかわらずアウトカムが平均$${\mu}$$，分散$${\sigma^2}$$の正規分布に従うという信念が反映されています。パラメータの事後分布は，効果なしモデル$${\mathcal{M}_0}$$が仮定されていることを明示的に書くと，

$$
p(\mu, \sigma^2 \vert \bm y, \mathcal{M}_0)=\dfrac{p(\bm y \vert \mu, \sigma^2, \mathcal{M}_0)p(\mu, \sigma^2 \vert \mathcal{M}_0)}{p(\bm y \vert \mathcal{M}_0)}
$$

と表せます。

　ここで，2つのモデル$${\mathcal{M}_1}$$と$${\mathcal{M}_0}$$を比較する方法について考えてみましょう。ベイズ統計学では，パラメータの事後分布を推定するのと同じ形式で，モデルの事後確率を推定することができます。効果ありモデル$${\mathcal{M}_1}$$の事前確率を$${p(\mathcal{M}_1)}$$と置くと，データ$${\bm y}$$が観測された後の$${\mathcal{M}_1}$$の事後モデル確率$${p(\mathcal{M}_1\vert \bm y)}$$は，ベイズの定理を使って

$$
p(\mathcal{M}_1 \vert \bm y)=\dfrac{p(\bm y \vert \mathcal{M}_1)p(\mathcal{M}_1)}{p(\bm y)}
$$

と表せます[4]。同様に，$${\mathcal{M}_0}$$の事後モデル確率$${p(\mathcal{M}_0 \vert \bm y)}$$は

$$
p(\mathcal{M}_0 \vert \bm y)=\dfrac{p(\bm y \vert \mathcal{M}_0)p(\mathcal{M}_0)}{p(\bm y)}
$$

と表せます。これらの事後モデル確率を利用してモデルを評価することもできますが，通常は，事前モデル確率に依存しない指標として，各式の右辺の分子にある$${p(\bm y \vert \mathcal{M}_1)}$$と$${p(\bm y \vert \mathcal{M}_0)}$$の比を考えます。この$${p(\bm y \vert \mathcal{M}_1)}$$と$${p(\bm y \vert \mathcal{M}_0)}$$は，先に示したパラメータの事後分布の式で右辺の分母にあった周辺尤度と同じもので，データが各モデルに対して持つ相対的な証拠の大きさとして解釈することができます。あるいは，事前に立てた仮説 (モデル) の予測と実際に観測されたデータがどのくらい整合的であるかを表す指標 (事前予測の良さ) と考えることもできます[5]。2つのモデルを比較する場合には，周辺尤度の比であるベイズファクターを利用するのが一般的です。ベイズファクターの値は，事後モデルオッズ (事後モデル確率の比) が事前モデルオッズ (事前モデル確率の比) の何倍であるかを意味します。

　ベイズファクターを使うことで，関心のある2つの仮説，すなわち効果ありモデル$${\mathcal{M}_1}$$と効果なしモデル$${\mathcal{M}_0}$$を比較することができます。ただし，ベイズ推定を行うためにはパラメータの事前分布を先に決めておく必要があります。2つのモデルに共通して含まれるパラメータの事前分布はベイズファクターにあまり影響しないので，$${\mathcal{M}_1}$$と$${\mathcal{M}_0}$$に共通のパラメータである$${\mu}$$と$${\sigma^2}$$に関しては，無情報な事前分布として

$$
\mu \sim \textrm{Normal}(0,100^2) \\
p(\sigma^2 ) \propto \dfrac{1}{\sigma^2}
$$

を設定することにしましょう[6]。問題となるのは$${\mathcal{M}_1}$$だけに含まれる標準化平均値差$${\delta}$$の事前分布です。ここではとりあえず，RのBayesFactorパッケージのデフォルト設定 (Morey et al., 2024) に倣い，位置パラメータが$${0}$$，スケールパラメータが$${\sqrt{2}/2}$$のコーシー分布を事前分布とし，

$$
\delta \sim \textrm{Cauchy}(0,\dfrac{\sqrt{2}}{2})
$$

と置くことにします。$${\mathcal{M}_0}$$と$${\mathcal{M}_1}$$の違いは，$${\delta}$$を0に固定するか，$${\delta}$$が$${0}$$以外の値を取ることを許容するかの違いです。周辺尤度の比であるベイズファクターが$${\mathcal{M}_0}$$よりも$${\mathcal{M}_1}$$を支持する方向に大きければ ($${{BF}_{10}>1}$$)，介入の効果があるという仮説がデータから相対的に支持されたことになります。介入の効果が実際にあるという仮定のもとで生成した人工データを使ってベイズファクターを計算してみたところ，$${{BF}_{10}=p(\bm y \vert \mathcal{M}_1)/p(\bm y \vert \mathcal{M}_0 )=4.04}$$となり，介入ありモデル$${\mathcal{M}_1}$$が介入なしモデル$${\mathcal{M}_0}$$よりも支持されるという「正しい」結果が得られました。$${{BF}_{10}=4.04}$$という値は，Jeffreys (1961) の基準に照らすと実質的な (substantial) 証拠として解釈できます。

　ただし，ベイズファクターはあくまでも相対的な評価指標であることには留意が必要です。たとえ効果なしモデル$${\mathcal{M}_0}$$を支持する結果 ($${{BF}_{10}<1}$$) が得られたとしても，介入効果がないという仮説を支持する絶対的な証拠とみなすことはできませんし，そもそも現実的には平均値差が厳密に$${\delta=0}$$であるということはほぼあり得ません。$${\mathcal{M}_1}$$と比べて$${\mathcal{M}_0}$$の方がマシであれば，厳密に$${\delta=0}$$でなくても$${\mathcal{M}_0}$$は支持されますし，比較対象である$${\mathcal{M}_1}$$によっては結果が逆転するということもあり得ます。今回のケースでも，ベイズファクターの値は$${\mathcal{M}_1}$$における$${\delta}$$の事前分布に大きく依存します。

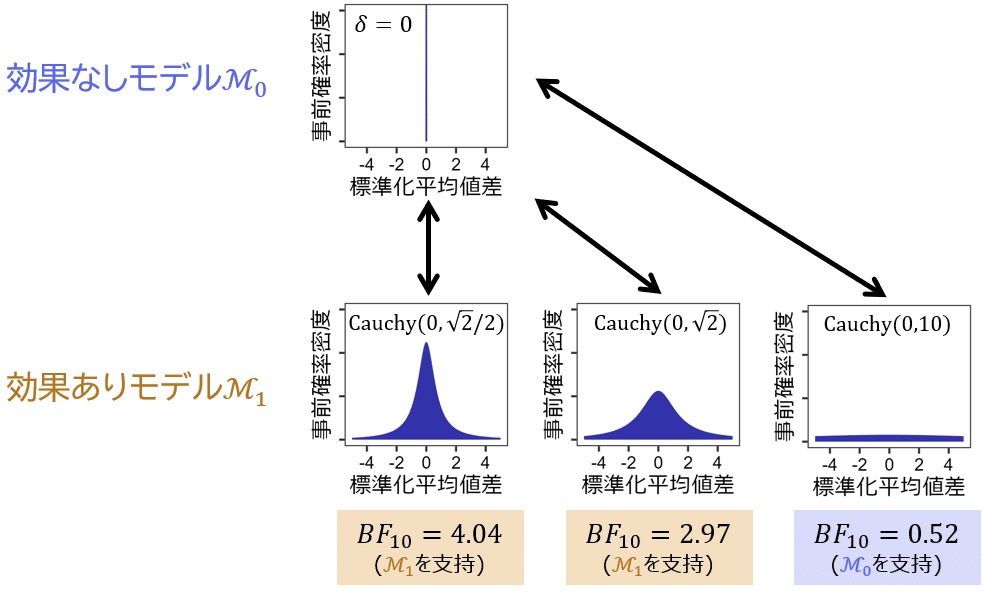
　上の図は，$${\delta}$$の事前分布として設定したコーシー分布のスケールパラメータ (分布の幅の広さ) を変えたときのベイズファクターの違いを示しています。事前分布のスケールパラメータが大きく分布の幅が広いほど効果なしモデル$${\mathcal{M}_0}$$が支持されやすいということがこの結果から読み取れます。幅の狭い事前分布を設定したモデルはデータに対する強い (狭い) 予測をするため，実際に観測されたデータが予測の範囲内かどうかによって周辺尤度が大きく変化しますが，幅の広い事前分布を持つモデルはどんなデータでもある程度予測できてしまうため，実際のデータによらず周辺尤度が小さな値を取りやすく，結果的に他のモデルと比べて支持されにくくなります。これは，冗長なパラメータ空間を持つモデルにはペナルティが与えられるという「ベイズ的オッカムの剃刀」の一例と見ることができます。したがって，ベイズファクターを利用して仮説を評価する際には事前分布の設定に気を配る必要があります。特にモデル間の重要な差異をもたらすパラメータに関しては無情報事前分布の利用は避けなくてはなりません。複数の事前分布を試して結果を比較する感度分析を実施するのもよいでしょう。

4. パラメータ推定アプローチ：方向性確率 (pd)

　パラメータに関する仮説に関心がある場合には，データから推定されたパラメータの事後分布を利用してその仮説を評価する方法も利用できます。介入効果の有無に関心がある場合，前節で利用した効果ありモデル$${\mathcal{M}_1}$$を使って$${\delta}$$の事後分布を推定し，その事後分布の情報から$${\delta}$$を$${0}$$とみなせるか否かを判断します。直観的には，$${\delta}$$の事後分布における$${\delta=0}$$の確率密度が相対的に十分小さく，事後分布が全体として$${0}$$から離れた位置に広がっていれば，介入の効果があると言えそうです。

　事後分布を利用した仮説の評価指標としてはさまざまなものが提案されていますが，ここでは心理学と比較的相性がよいと思われる汎用的な指標として，Makowski (2019) が提案した効果の存在の指標である方向性確率 (probability of direction; pd) を紹介します。

　方向性確率は，パラメータがその事後分布の中央値と同じ符号である確率として定義されます。分かりやすくいえば，パラメータの値が$${0}$$を下回る確率$${p(\delta<0)}$$と$${0}$$を上回る確率$${p(\delta >0)}$$のうち大きい方が方向性確率です。定義より，方向性確率は$${.5}$$から$${1}$$までの範囲を取りえます。効果が実際に存在する場合，データ数が十分であれば，効果を表すパラメータの事後分布は$${0}$$から離れる方向にシフトすると期待されるため，方向性確率は$${1}$$に近い値となります。

　伝統的な頻度主義統計学では$${\delta=0}$$のような帰無仮説を立てて$${p}$$値を計算しますが，方向性確率はこの$${p}$$値とよく似た振る舞いをします。実際，対応のない$${t}$$検定に相当するモデルのような比較的単純なモデルであれば，パラメータの事前分布に幅の広い一様分布を仮定したとき，両側検定の$${p}$$値と方向性確率 (pd) は一対一に対応し，その関係は

$$
pd=1-\dfrac{p}{2}
$$

と表すことができます。例えば，$${p=.05}$$は$${pd=.975}$$と対応します。また，方向性確率は$${p}$$値と同様，効果の存在を示す証拠としては利用できますが，効果の不在を示すのには使えないという非対称性があります (詳しくはMakowski, 2019を参照してください)。$${p}$$値に慣れ親しんできた研究者にとって方向性確率は比較的分かりやすくて使いやすい指標と言えるかもしれません。

　パラメータ推定アプローチには，モデル比較アプローチと比べてパラメータの事前分布の影響を受けにくいという利点があります。これは，データ数が十分多ければ，事後分布に対する事前分布の影響が相対的に弱まることに起因します。また，パラメータの事前分布として範囲が$${(-\infty, \infty)}$$の一様分布のようなimproper[7]な無情報事前分布を用いることもできます。

　本稿ではパラメータ推定アプローチとして方向性確率 (pd) を取り上げましたが，事後分布を用いた仮説の評価指標は他にもあります。例えば，効果の有無を判断するためのパラメータの範囲に関する理論的・実践的な知識を利用できる場合には，Kruschke (2014 前田・小杉監訳 2017) などで紹介されている，実践的に等価な領域 (region of practical equivalence; ROPE) を利用することができます。また，豊田 (2022) は，事後分布から事後確率を計算する際の範囲や基準点を1つに固定するのではなく，範囲や基準点を変化させたときの確率も吟味したうえで実質科学的な観点から効果の程度を議論することを推奨しています。このように，パラメータ推定アプローチに関してはさまざまな方法が提案されていますが，ベイズファクターと比較すると，事後分布の評価の仕方に関するコンセンサスは心理学ではまだ十分得られていないように思われます。

5. まとめ

　本記事では心理学におけるベイズ統計学を利用した仮説評価の指標として，モデル比較アプローチの周辺尤度およびベイズファクターと，パラメータ推定アプローチの方向性確率 (pd) に焦点を当てて解説しました。はじめにも述べたように，ベイズ統計学は頻度主義統計学と同様，研究において必ずしも適切に利用されている訳ではありません (e.g., Sawada, 2023; Tendeiro et al., 2024)。私自身も論文を読んだり査読をしたりする中で，事前分布やモデルの設定が不適切であったり，報告すべき情報が論文中で報告されていなかったり，結果の解釈に問題があったりといった事例をこれまでにいくつも見てきました。このような状況の打開に少しでも役立つことを願って，本記事では本邦の心理学者やデータ分析に携わる人に向けてなるべく分かりやすくコンパクトにベイズ統計学による仮説評価の方法のエッセンスを整理・解説しようと試みました。ソフトウェアを用いた評価指標の計算方法などデータ分析の具体的・実践的な方法については本記事では扱いませんでしたが，関心のある方は馬場 (2019) や浜田・石田・清水 (2019) などの良著を参考にしてください。

脚注

1. ただし，見かけ上は仮説演繹法を遵守しているように見えても，実際にはそうではない研究が少なくなく，それが心理学の再現可能性を低めているという主張もあります (Chambers, 2017 大塚訳 2019)。

2. 事前分布もモデルの一部であると考えることもあります。分野によっては右辺の分子全体を生成モデル (generative model) と呼ぶことがあります。

3. ここでは単純さを重視して等分散性を仮定していますが，群ごとに分散が異なることを仮定してもかまいません。

4. 本記事では，確率密度を返す関数と確率を返す関数を区別せず，どちらも $${p(\cdot)}$$で表しています。

5. 事前予測の良さではなく事後予測の良さ (今回推定されたモデルで将来のデータをどのくらい予測できるか) に関心がある場合は，交差検証やWAICなどを利用して汎化性能を評価するのが一般的です。

6. ここで設定した$${\sigma}$$の事前分布はJeffreys priorと呼ばれる無情報事前分布の一種で，スケール変換に対する不変性を持ちます。今回の設定の場合，代わりに$${\textrm{Uniform}(0, 100)}$$のような事前分布を与えても結果はほとんど変わりません。

7. 定義域上で積分しても$${1}$$にならない事前分布をimproperな事前分布と呼びます。先述の通り，ベイズファクターを計算する際にはimproperな事前分布の使用は問題になりえます。

引用文献

• 馬場 真哉 (2019). RとStanではじめる　ベイズ統計モデリングによるデータ分析入門　講談社

• Chambers, C. (2017). The Seven Deadly Sins of Psychology: A Manifesto for Reforming the Culture of Scientific Practice. Princeton University Press.
  (チェインバーズ, C. 大塚 紳一郎 (訳) (2019). 心理学の7つの大罪――真の科学であるために私たちがすべきこと――　みすず書房)

• 浜田 宏・石田 淳・清水 裕士 (2019). 社会科学のためのベイズ統計モデリング　朝倉書店

• Jeffreys, H. (1961). The Theory of Probability (3rd ed.). Oxford University Press.

• Kruschke, J. K. (2014). Doing Bayesian Data Analysis: A Tutorial with R, JAGS, and Stan (2nd ed.). ‎ Academic Press.
  (Kruschke, J. K. 前田 和寛・小杉 考司 (監訳) (2017). ベイズ統計モデリング――R，JAGS，Stanによるチュートリアル――　共立出版)

• Makowski, D., Ben-Shachar, M. S., Chen, S. H. A., & Lüdecke, D. (2019). Indices of effect existence and significance in the Bayesian framework. Frontiers in Psychology, 10, Article 2767. https://doi.org/10.3389/fpsyg.2019.02767

• Morey, R. D., & Rouder, J. N. (2024). BayesFactor: Computation of Bayes factors for common designs. https://CRAN.R-project.org/package=BayesFactor

• Sawada, T. (2023). Effects of violating the assumptions of equal variance and independent and identically distributed random variables: A case using Bayesian statistical modeling. The Quantitative Methods for Psychology, 19(3), 281-295. https://doi.org/10.20982/tqmp.19.3.p281

• Tendeiro, J. N., Kiers, H. A. L., Hoekstra, R., Wong, T. K., & Morey, R. D. (2024). Diagnosing the misuse of the Bayes factor in applied research. Advances in Methods and Practices in Psychological Science, 7(1), 1–19. https://doi.org/10.1177/25152459231213371

• 豊田 秀樹 (2022). 統計学入門Ⅰ――生成量による実感に即したデータ分析――　朝倉書店

執筆者プロフィール

著訳書